题目内容
 如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.
如图,将矩形ABCD沿BD对折,点A落在E处,BE与CD相交于F,若AD=3,BD=6.(1)求证:△EDF≌△CBF;
(2)求∠EBC.
考点:翻折变换(折叠问题),全等三角形的判定与性质,矩形的性质
专题:证明题
分析:(1)首先根据矩形的性质和折叠的性质可得DE=BC,∠E=∠C=90°,对顶角∠DFE=∠BFC,利用AAS可判定△DEF≌△BCF;
(2)在Rt△ABD中,根据AD=3,BD=6,可得出∠ABD=30°,然后利用折叠的性质可得∠DBE=30°,继而可求得∠EBC的度数.
(2)在Rt△ABD中,根据AD=3,BD=6,可得出∠ABD=30°,然后利用折叠的性质可得∠DBE=30°,继而可求得∠EBC的度数.
解答:(1)证明:由折叠的性质可得:DE=BC,∠E=∠C=90°,
在△DEF和△BCF中,
,
∴△DEF≌△BCF(AAS);
(2)解:在Rt△ABD中,
∵AD=3,BD=6,
∴∠ABD=30°,
由折叠的性质可得;∠DBE=∠ABD=30°,
∴∠EBC=90°-30°-30°=30°.
在△DEF和△BCF中,
|
∴△DEF≌△BCF(AAS);
(2)解:在Rt△ABD中,
∵AD=3,BD=6,
∴∠ABD=30°,
由折叠的性质可得;∠DBE=∠ABD=30°,
∴∠EBC=90°-30°-30°=30°.
点评:本题考查了折叠的性质、矩形的性质,以及全等三角形的判定与性质,正确证明三角形全等是关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
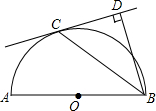 如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.
如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.
 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=
如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=