Question

【题目】如图，与均为正三角形，且顶点、均在双曲线上，点、在轴上，连结交于点，则的面积是

A. B. C. D.

Answer 1

【答案】C

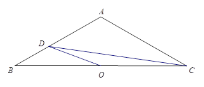
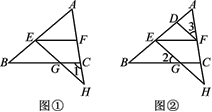
【解析】分析：先根据△AOB和△ACD均为正三角形可知∠AOB=∠CAD=60°，故可得出AD∥OB，所以S△ABP=S△AOP，故S△OBP=S△AOB，过点B作BE⊥OA于点E，由反比例函数系数k的几何意义即可得出结论．

详解：∵△AOB和△ACD均为正三角形， ∴∠AOB=∠CAD=60°，∴AD∥OB，

∴S△ABP=S△AOP， ∴S△OBP=S△AOB，

过点B作BE⊥OA于点E，则S△OBE=S△ABE=S△AOB，

∵点B在反比例函数y=的图象上， ∴S△OBE=×4=2， ∴S△OBP=S△AOB=2S△OBE=4．故选C．