题目内容
Rt△ABC中，∠ACB=90°，AC=2
cm，BC=
cm，求AB上的高CD长度．
解：在Rt△ABC中，
由勾股定理得：AB=
=3，
由面积公式得：S△ABC=1
AC•BC=AB•CD，
∴CD=
=
．
分析：先用勾股定理求出斜边AB的长度，再用面积就可以求出斜边上的高．
点评：利用勾股定理和直角三角形的面积相结合，求解斜边上的高是解直角三角形的重要题型之一，也是中考的热点．
由勾股定理得：AB=
=3，由面积公式得：S△ABC=1
AC•BC=AB•CD，∴CD=
=．分析：先用勾股定理求出斜边AB的长度，再用面积就可以求出斜边上的高．
点评：利用勾股定理和直角三角形的面积相结合，求解斜边上的高是解直角三角形的重要题型之一，也是中考的热点．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
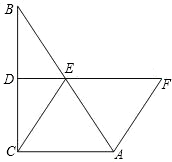延长线上，且AF=CE．求证：四边形ACEF是菱形．
如图，在Rt△ABC中，∠BAC=90°，点D、E、F分别是三边的中点，且CF=3cm，则DE=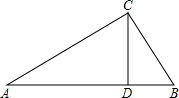
如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD=
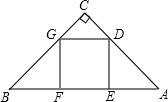点G在边BC上．
如图，Rt△ABC中，∠C=90°，D为AB的中点，DE⊥AB，AB=20，AC=12，则四边形ADEC的面积为