题目内容
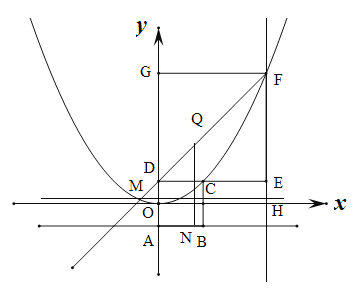
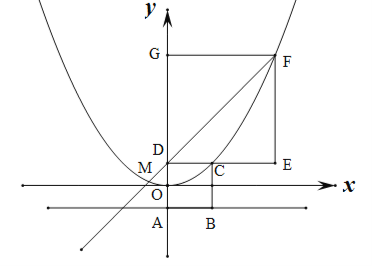
【题目】(本题满分10分)如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为![]() ,点A、D、G在
,点A、D、G在![]() 轴上,坐标原点O为AD的中点,抛物线
轴上,坐标原点O为AD的中点,抛物线![]() 过C、F两点,连接FD并延长交抛物线于点M.
过C、F两点,连接FD并延长交抛物线于点M.
(1)若![]() ,求m和b的值;
,求m和b的值;
(2)求![]() 的值;
的值;
(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由.
【答案】(1)m=![]() ,b=1+
,b=1+![]() (2)
(2)![]() =1+
=1+![]() (3)以FM为直径的圆与AB所在的直线相切
(3)以FM为直径的圆与AB所在的直线相切
【解析】
试题分析:(1)由a代入可求C,再根据待定系数法可求得m值,然后把F点坐标代入可求b;
(2)把C(2a,a)、F(2b,2b+1)代入y=![]() 得可求得
得可求得![]() =1+
=1+![]() ;
;
(3)由C、F、D的坐标可求得m=![]() ,然后可求得用a表示的F点的坐标,求出直线MF的解析式,代入二次函数,求得M点的坐标,然后过M作x轴的平行线,过F作y轴平行线相交于点H,取MF得中点Q,做垂线QN垂直AB 与N,交MH于P.在等腰直角三角形MFH中,求得QN=
,然后可求得用a表示的F点的坐标,求出直线MF的解析式,代入二次函数,求得M点的坐标,然后过M作x轴的平行线,过F作y轴平行线相交于点H,取MF得中点Q,做垂线QN垂直AB 与N,交MH于P.在等腰直角三角形MFH中,求得QN=![]() FM,进而得出结论.
FM,进而得出结论.
试题解析:解:(1)∵a=1
∴把C(2,1)代入y=![]() 得4m=1
得4m=1
∴m=![]()
把F(2b,2b+1)代入![]() 得
得![]()
解得b=1±![]()
负值舍去,所以b=1+![]()
(2)把C(2a,a)、F(2b,2b+1)代入y=![]() 得
得
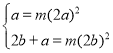
消去m得![]()
∴![]()
故![]() =1±
=1±![]()
∴![]() =1+
=1+![]()
以FM为直径的圆与AB所在的直线相切,理由如下:
C(2a,a)、F(2b,2b+1)、D(0,a)
把C(2a,a)代入y=![]() 得a=m
得a=m![]()
∴m=![]()
由(2)的结果![]() =1+
=1+![]() 可得
可得![]()
故F(2a+2![]() a,3a+2
a,3a+2![]() a)
a)
设MF:y=kx+a(k>0)
把F点坐标代入得k=1
所以MF得解析式为y=x+a
将y=x+a代入![]() ,解得x=2a±2
,解得x=2a±2![]() a
a
所以M(2a-2![]() a,3a-2
a,3a-2![]() a)
a)
过M作x轴的平行线,过F作y轴平行线相交于点H,取MF得中点Q,做垂线QN垂直AB 与N,交MH于P.
在等腰直角三角形MFH中,MH=FH=4![]() a
a
∴MF=8a
QN=2![]() a+(3a-2
a+(3a-2![]() a)+a=4a
a)+a=4a
故QN=![]() MF
MF
所以以FM为直径的圆与直线AB相切.