Question

【题目】如果一个直角三角形的三边长分别为，则称这个三角形均匀直角三角形．

（1）判定按照上述定义，下列长度的三条线段能组成均匀直角三角形的是（）

A．1，2，3 B．1,1,2 C．2,3,4 D．3，4，5，

（2）性质求证：任何均匀直角三角形的较小直角边与较大直角边的比是

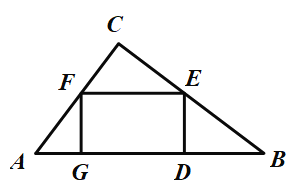
（3）应用如图，在一块均匀直角三角形纸板中剪一个矩形，且矩形的一边在上，其余两个顶点分别在上，已知，求剪出矩形面积的最大值．

Answer 1

【答案】（1）D；（2）见解析；（3）

【解析】

(1)根据均匀直角三角形的定义分别验证四个选项即可得到答案；

(2)根据题意得到，再展开计算化简即可得到任何均匀直角三角形的较小直角边与较大直角边的比是；

(3) 过点作，交于点，根据均匀三角形的定义求出CH的长度，设为，矩形面积为，证，根据相似三角形的性质以及二次函数的性质求出y的最大值即可得到答案；

解：（1）A．1，2，3因为 ，故三角形不是直角三角形，进而不是均匀直角三角形；

B．1,1,2因为 ，故三角形不是直角三角形，进而不是均匀直角三角形；

C．2,3,4因为 ，故三角形不是直角三角形，进而不是均匀直角三角形；

D．3，4，5满足，且满足三边的关系为：，故是均匀直角三角形；

故选：D；

（2）证明：由题意得

，

，

（3）过点作，交于点，

在均匀直角三角形纸板中，，

．

又

设为，矩形面积为，则：

在矩形中，

∴

即

矩形面积的最大值为．