题目内容
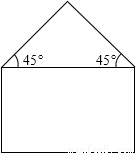
用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.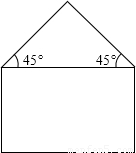
【答案】分析:由特殊等腰直角三角形,设出直角边长,再表示其它各边边长,把金属框围成的面积用未知量x表示出来,转化为求函数最值问题,从而求出金属框围成的图形的最大面积.
解答:解:根据题意可得,等腰直角三角形直角边长为 m,矩形的一边长为2xm,
m,矩形的一边长为2xm,
其相邻边长为 =[
=[ ]m,
]m,
∴该金属框围成的面积S=
 =-
=- (
( )
)
当x=- =
= 时,金属围成的面积最大,
时,金属围成的面积最大,
此时斜边长2x=( )m,
)m,
相邻边长为10-(2+ )
) =(
=( )m,
)m,
S最大=100(3-2 )=(300-200
)=(300-200 )m2.
)m2.
答:矩形的相邻两边长各为(60-40 )m,(10
)m,(10 -10)m,金属框围成的图形的最大面积为:(300-200
-10)m,金属框围成的图形的最大面积为:(300-200 )m 2.
)m 2.
点评:此题考查二次函数的性质及其应用,将实际问题转化为求函数最值问题,从而来解决实际问题,比较简单.
解答:解:根据题意可得,等腰直角三角形直角边长为
 m,矩形的一边长为2xm,
m,矩形的一边长为2xm,其相邻边长为
 =[
=[ ]m,
]m,∴该金属框围成的面积S=

 =-
=- (
( )
)当x=-
 =
= 时,金属围成的面积最大,
时,金属围成的面积最大,此时斜边长2x=(
 )m,
)m,相邻边长为10-(2+
 )
) =(
=( )m,
)m,S最大=100(3-2
 )=(300-200
)=(300-200 )m2.
)m2.答:矩形的相邻两边长各为(60-40
 )m,(10
)m,(10 -10)m,金属框围成的图形的最大面积为:(300-200
-10)m,金属框围成的图形的最大面积为:(300-200 )m 2.
)m 2.点评:此题考查二次函数的性质及其应用,将实际问题转化为求函数最值问题,从而来解决实际问题,比较简单.

练习册系列答案
相关题目
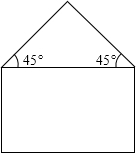 用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.
用长度为20m的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2xm.当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.