题目内容
18.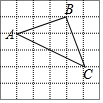 已知△ABC顶点都在4×4的正方形网格格点上,如图所示.
已知△ABC顶点都在4×4的正方形网格格点上,如图所示.(1)请画出△ABC的外接圆,并标明圆心O的位置;
(2)这个圆中弦BC所对的圆周角的度数是45°或135°.
分析 (1)先根据勾股定理判断出△ABC的形状,进而可画出其外接圆与圆心;
(2)由圆周角定理即可得出结论.
解答  解:(1)如图,∵AB=AC=$\sqrt{10}$,AC=$\sqrt{20}$,
解:(1)如图,∵AB=AC=$\sqrt{10}$,AC=$\sqrt{20}$,
∴△ABC是等腰直角三角形,
∴⊙O即为所求;
(2)∵△ABC是等腰直角三角形,
∴∠A=45°,
∴∠A′=180°-45°=135°.
故答案为:45°或135°.
点评 本题考查的是作图-复杂作图,熟知外接圆的作法是解答此题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
8.如果|a-1|+(b+2)2=0,则(a+b)2016的值是( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
9.方程x2-22x+2=0的根的情况为( )
| A. | 有一个实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 有两个相等的实数根 |
6.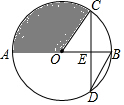 如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,且E为OB的中点,CD=4$\sqrt{3}$,则图中阴影部分的面积为( )| A. | π | B. | 4π | C. | $\frac{4}{3}$π | D. | $\frac{16}{3}$π |
13. 如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为( )
如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为( )
 如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为( )
如图,已知A,B,C为⊙O上三点,若∠AOB=80°,则∠ACB度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 40° |
10.下列各数中,比-2小的数是( )
| A. | -3 | B. | -1 | C. | 1 | D. | 0 |
7. 实数b在数轴上的位置如图所示,则实数b可能的取值为( )
实数b在数轴上的位置如图所示,则实数b可能的取值为( )
 实数b在数轴上的位置如图所示,则实数b可能的取值为( )
实数b在数轴上的位置如图所示,则实数b可能的取值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{7}$-2 |
8.函数y=$\sqrt{4-3x}$的自变量x的取值范围是( )
| A. | x<4 | B. | x<$\frac{4}{3}$ | C. | x≤4 | D. | x≤$\frac{4}{3}$ |