题目内容
 在10×10的正方形网格中,小正方形的边长为1,建立如图所示的直角坐标系:
在10×10的正方形网格中,小正方形的边长为1,建立如图所示的直角坐标系:(1)△ABC关于y轴对称的三角形是△A′B′C′,以O为旋转中心,将△A′B′C′顺时针旋转90°得到△A′′B′′C′′则A′′的坐标是
(4,-2)
(4,-2)
;(2)计算A′旋转到A′′所经过的路线长是
5π
5π
.分析:(1)根据轴对称变换:由一个平面图形得到它的轴对称图形叫做轴对称变换.
根据旋转变换的定义:把一个图形绕着某一点O按照一定的方向转动一个角度的图形变换叫做旋转.点O叫做旋转中心,转动的方向叫做旋转方向,转动的角度叫做旋转角.旋转的“三要素”:旋转中心、旋转方向、旋转角度,缺一不可.
根据平面直角坐标系写出A′′的坐标.
(2)根据勾股定理计算OA′的长,再根据弧长公式求出A′旋转到A′′所经过的路线长.
根据旋转变换的定义:把一个图形绕着某一点O按照一定的方向转动一个角度的图形变换叫做旋转.点O叫做旋转中心,转动的方向叫做旋转方向,转动的角度叫做旋转角.旋转的“三要素”:旋转中心、旋转方向、旋转角度,缺一不可.
根据平面直角坐标系写出A′′的坐标.
(2)根据勾股定理计算OA′的长,再根据弧长公式求出A′旋转到A′′所经过的路线长.
解答:解:(1)如图所示.
 A′′(4,-2)
A′′(4,-2)
(2)A′A′′=5π
 A′′(4,-2)
A′′(4,-2)(2)A′A′′=5π
点评:成轴对称的两个图形可以看作是其中一个图形由另一个图形经过轴对称变换后得到的;一个轴对称图形也可以看作是由它的一部分图形,经过轴对称变换形成的.旋转的性质:(1)旋转前后的图形是全等形;(2)旋转前后的对应点与旋转中心组成的角都相等,都为旋转角;(3)对应点到旋转中心的距离相等.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
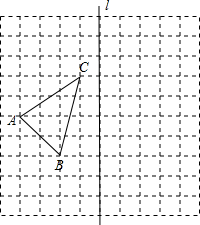 (2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上). (2009•滨湖区一模)如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.
(2009•滨湖区一模)如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上. 如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位.将△ABC沿着BC翻折得到△DBC,把△DBC向下平移3个单位得到△D1B1C1,再把△D1B1C1绕点C1顺时针旋转90°得到△D2B2C2.请你分别画出△DBC、△D1B1C1和△D2B2C2(不要求写画法)
如图,在10×10的正方形网格中,每个小正方形的边长均为1个单位.将△ABC沿着BC翻折得到△DBC,把△DBC向下平移3个单位得到△D1B1C1,再把△D1B1C1绕点C1顺时针旋转90°得到△D2B2C2.请你分别画出△DBC、△D1B1C1和△D2B2C2(不要求写画法) 如图,在10×10的正方形网格纸中(每个小方格的边长都是1个单位)有一个△ABC,请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′.
如图,在10×10的正方形网格纸中(每个小方格的边长都是1个单位)有一个△ABC,请在网格纸中画出以点O为旋转中心把△ABC按顺时针方向旋转90°得到的△A′B′C′.