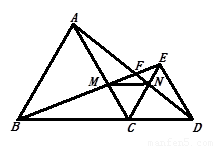题目内容
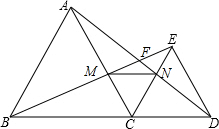 如图,点C在BD上,在线段BD的同侧作等边△ABC和等边△CDE,AD、BE相交于点F.
如图,点C在BD上,在线段BD的同侧作等边△ABC和等边△CDE,AD、BE相交于点F.(1)求证:BE=AD;
(2)求∠AFB的度数;
(3)设BE与AC交于点M,CE与AD交于点N,连接MN,试判断△MCN的形状,并说明理由.
分析:(1)由等边三角形的性质就可以得出AC=BC,DC=EC,就可以得出△ACD≌△BCE而得出结论;
(2)由△ACD≌△BCE可以得出∠CAD=∠CBE,由外角与内角的关系就可以得出结论;
(3)由条件通过证明△ACN≌△BCM就可以得出CN=CM,就可以得出结论.
(2)由△ACD≌△BCE可以得出∠CAD=∠CBE,由外角与内角的关系就可以得出结论;
(3)由条件通过证明△ACN≌△BCM就可以得出CN=CM,就可以得出结论.
解答:解:(1)∵△ABC和△CDE都是等边三角形,
∴AC=BC,DC=EC,∠ACB=∠DCE=60°.
∴∠ACB+∠ACE=∠DCE+∠ACE,
∴∠ACD=∠BCE.
∵,∠ACB+∠DCE+∠ACE=180°,
∴∠ACE=60°.
∴∠ACE=∠ACB.
在△ACD和△BCE中
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠AFB=∠CBE+∠BDF,
∴∠AFB=∠CAD+∠BDF.
∵∠CAD+∠BDF=∠ACB=60°,
∴∠AFB=60°;
(3)∴△CNM为等边三角形理由:
在△ACN和△BCM中
,
∴△ACN≌△BCM(ASA),
∴CN=CM.
∵∠ACE=60°,
∴△CNM为等边三角形.
∴AC=BC,DC=EC,∠ACB=∠DCE=60°.
∴∠ACB+∠ACE=∠DCE+∠ACE,
∴∠ACD=∠BCE.
∵,∠ACB+∠DCE+∠ACE=180°,
∴∠ACE=60°.
∴∠ACE=∠ACB.

在△ACD和△BCE中
|
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠AFB=∠CBE+∠BDF,
∴∠AFB=∠CAD+∠BDF.
∵∠CAD+∠BDF=∠ACB=60°,
∴∠AFB=60°;
(3)∴△CNM为等边三角形理由:
在△ACN和△BCM中
|
∴△ACN≌△BCM(ASA),
∴CN=CM.
∵∠ACE=60°,
∴△CNM为等边三角形.
点评:本题考查了全都呢过三角形的判定与性质的运用,等式的性质的运用,等边三角形的判定与性质的运用,三角形外角与内角的挂席的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
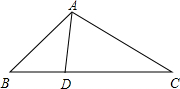 如图:点D在BC上,∠BAC=∠ADB,AB=2,BC=4,则BD等于( )
如图:点D在BC上,∠BAC=∠ADB,AB=2,BC=4,则BD等于( )A、
| ||
B、
| ||
| C、1 | ||
D、
|
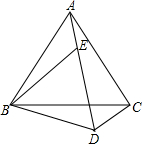 如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由.
如图,点E在AD上,△ABC和△BDE都是等边三角形.猜想:BD、CD、AD三条线段之间的关系,并说明理由. 如图,点D在AC上,且AB=AC,BC=BD=AD,则∠A=
如图,点D在AC上,且AB=AC,BC=BD=AD,则∠A=