Question

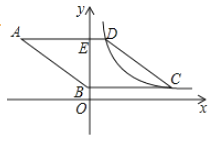
【题目】如图，是等腰三角形，，点是上一点，过点作交于点，交延长线于点．

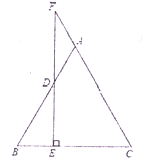
（1）证明：是等腰三角形；

（2）若，，，求的长．

Answer 1

【答案】（1）见详解 （2）4

【解析】

（1）由AB=AC，可知∠B=∠C，再由DE⊥BC，可知∠F+∠C=90°，∠BDE+∠B=90，然后余角的性质可推出∠F=∠BDE，再根据对顶角相等进行等量代换即可推出∠F=∠FDA，于是得到结论；
（2）根据解直角三角形和等边三角形的性质即可得到结论．

证明：（1）∵AB=AC

∴∠B=∠C，

∵FE⊥BC，

∴∠F+∠C=90°，∠BDE+∠B=90°，

∴∠F=∠BDE，

又∵∠BDE=∠FDA，

∴∠F=∠FDA，

∴AF=AD，

∴△ADF是等腰三角形；

（2）∵DE⊥BC，

∴∠DEB=90°,

∵∠B=60°,BD=4，

∴BE=BD=2

∵AB=AC

∴△ABC是等边三角形，

∴BC=AB=AD+BD=6，

∴EC=BC-BE=4