Question

【题目】某班“数学兴趣小组”对函数的图象与性质进行了探究，探究过程如下，请补充完整．

（1）函数的自变量的取值范围是_________．

（2）下表是与的几组对应值．

	…				0			2	3	4	5	…
	…											…

则表格中的__________．

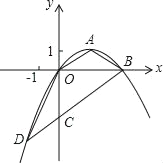
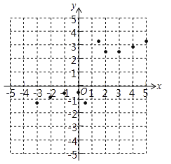
（3）如图，在平面直角坐标系中，描出了以上表格中各组对应值为坐标的点，请根据描出的点，画出该函数的图象；试写出该函数的一条性质________________________________________________________．

（4）①当直线与函数的图象有唯一交点时，的值为___________；

②若直线与函数无交点，则的取值范围为_____________．

Answer 1

【答案】（1）；（2）；（3）图详见解析，函数图象关于点中心对称（答案不唯一）；（4）①；②．

【解析】

（1）依据分母不为零即可得出自变量x的取值范围；

（2）依据自变量x的值，即可得到m的值；

（3）先通过描点画出该函数的图象即可得出该函数的一条性质；

（4）①根据一元二次方程的判别式等于0，即可得到m值；

②由①知当或时，直线与函数的图象有唯一交点，而直线可看作由直线上下平移得到，从而求出m的取值范围.

解：（1）∵x-1≠0,则；

（2）当x=4时，，则m=；

（3）画出该函数的图象如解图所示，

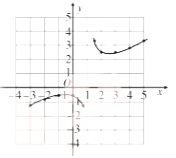
函数图象关于点中心对称．（答案不唯一）；

（4）①联立和，

得，

由题意，可知该一元二次方程有两个相等的实数根，

∴，解得或，

∵，∴；

②由①知当或时，直线与函数的图象有唯一交点，

而直线可看作由直线上下平移得到，

∴当时，直线与函数的图象没有交点．