题目内容
 如图,矩形OABC边OA长为1,边AB长为2,OC在数轴上,且点O与原点重合.以O为圆心,对角线OB的长为半径画弧,交负半轴于点D,则点D表示的实数是
如图,矩形OABC边OA长为1,边AB长为2,OC在数轴上,且点O与原点重合.以O为圆心,对角线OB的长为半径画弧,交负半轴于点D,则点D表示的实数是
- A.

- B.

- C.

- D.

A
分析:由矩形OABC,得到三角形ABO为直角三角形,由AB与OA的长,利用勾股定理求出OB的长,再由OD=OB,得出OD的长,又D在原点左侧,即可得出点D表示的实数.
解答:∵四边形OABC为矩形,
∴∠A=90°,
在Rt△AOB中,OA=1,AB=2,
根据勾股定理得:OB= =
= ,
,
又∵OD=OB,
∴OD= ,又D在原点O左侧,
,又D在原点O左侧,
则D表示的实数是- .
.
故选A
点评:此题考查了勾股定理,实数与数轴,以及矩形的性质,灵活运用勾股定理是解本题的关键.
分析:由矩形OABC,得到三角形ABO为直角三角形,由AB与OA的长,利用勾股定理求出OB的长,再由OD=OB,得出OD的长,又D在原点左侧,即可得出点D表示的实数.
解答:∵四边形OABC为矩形,
∴∠A=90°,
在Rt△AOB中,OA=1,AB=2,
根据勾股定理得:OB=
 =
= ,
,又∵OD=OB,
∴OD=
 ,又D在原点O左侧,
,又D在原点O左侧,则D表示的实数是-
 .
.故选A
点评:此题考查了勾股定理,实数与数轴,以及矩形的性质,灵活运用勾股定理是解本题的关键.

练习册系列答案
相关题目
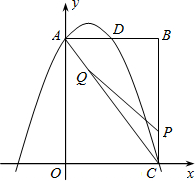
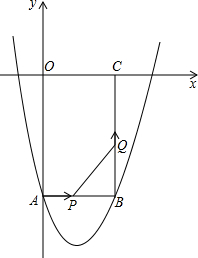 如图,矩形OABC边长OA、OC分别为12cm和6cm,点A、C分别在y轴和x轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
如图,矩形OABC边长OA、OC分别为12cm和6cm,点A、C分别在y轴和x轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.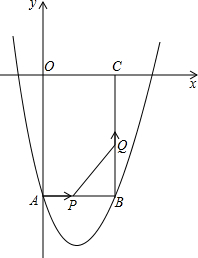 如图,矩形OABC边长OA、OC分别为12cm和6cm,点A、C分别在y轴和x轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
如图,矩形OABC边长OA、OC分别为12cm和6cm,点A、C分别在y轴和x轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.