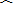题目内容
如图,已知AB是⊙O的直径,AD⊥DC,AC平分∠DAB.
(1﹚求证:直线CD与⊙O相切于点C;
(2﹚如果AD和AC的长是一元二次方程x2-(2+
)x+2
=0的两根,求AD、AC、AB的长和∠DAB的度数.

(1﹚求证:直线CD与⊙O相切于点C;
(2﹚如果AD和AC的长是一元二次方程x2-(2+
| 3 |
| 3 |

(1)证明:连接OC,
∵AD⊥DC,
∴∠ACD+∠CAD=90°,
∵OA=OC,
∴∠BAC=∠ACO,
又AC平分∠DAB,
∴∠CAB=∠CAD,
∴∠CAD=∠ACO,
∴∠ACD+∠ACO=90°,即OC⊥DC,
∴DC是⊙O的切线;
(2)方程x2-(2+
)x+2
=0,即(x-2)(x-
)=0,
解得:x1=
,x2=2,
∵AD<AC,∴AD=
,AC=2,
∴CD=
=1,
∵CD=
AC,
∴∠CAD=30°,
∴∠BAD=60°,
连接BC,
∵AB为直径,∴∠ACB=90°,
设BC=x,则AB=2x,
∴x2+22=(2x)2,
∵x>0,
∴x=
,
则AB=
.

∵AD⊥DC,
∴∠ACD+∠CAD=90°,
∵OA=OC,
∴∠BAC=∠ACO,
又AC平分∠DAB,
∴∠CAB=∠CAD,
∴∠CAD=∠ACO,
∴∠ACD+∠ACO=90°,即OC⊥DC,
∴DC是⊙O的切线;
(2)方程x2-(2+
| 3 |
| 3 |
| 3 |
解得:x1=
| 3 |
∵AD<AC,∴AD=
| 3 |
∴CD=
22-(
|
∵CD=
| 1 |
| 2 |
∴∠CAD=30°,
∴∠BAD=60°,
连接BC,
∵AB为直径,∴∠ACB=90°,
设BC=x,则AB=2x,
∴x2+22=(2x)2,
∵x>0,
∴x=
2
| ||
| 3 |
则AB=
4
| ||
| 3 |


练习册系列答案
相关题目




 点D,E为CH的中点,连接AE并延长交BD于F,直线CF交直线AB于点G.
点D,E为CH的中点,连接AE并延长交BD于F,直线CF交直线AB于点G.