��Ŀ����
7����1���Ķ����⣺�ڽ�һԪ���η���2x2-6x+4=0ʱ�������Ȱ���ߵĶ�������ʽ�ֽ���ʽ����2��x2-3x+2��=0����2��x-1����x-2��=0�������Ϳ��Եõ����̵���������x1=1��x2=2��������������Ҳ����������һԪ���η��������ķ������Ѷ�������ʽ�ֽ���ʽ�����ڶ�������ʽ2x2-6x+4=0�ֽ���ʽ����ʵ�����ǿ����������ʽ2x2-6x+4=0Ϊ0����һԪ���η���2x2-6x+4=0���ٽⷽ�̿ɵ�x1=1��x2=2���Ӷ��ɵ�2x2-6x+4=2��x-1����x-2����
��2��֪ʶǨ�ƣ�����ʵ����Χ�ڷֽ���ʽ��3x2-4x-1��
���� ��ԭʽ����0�����x��ֵ������ȷ�����ֽ�����
��� �⣺�ɷ���3x2-4x-1=0���ɽ�ã�x=$\frac{2��\sqrt{7}}{3}$��
��3x2-4x-1=3��x-$\frac{2+\sqrt{7}}{3}$����x-$\frac{2-\sqrt{7}}{3}$����
���� ���⿼����ʵ����Χ�ڷֽ���ʽ���Լ���һԪ���η���-��ʽ�ֽⷨ�������������㷨���ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
18����֪�߶�a=4��b=9���߶�x��a��b�ı��������x���ڣ�������
| A�� | 6 | B�� | 6��-6 | C�� | -6 | D�� | 36 |
12����֪���������εױ߳��������Ƿ���x2-9x+18=0����������������������ε��ܳ�Ϊ��������
| A�� | 15 | B�� | 12 | C�� | 15��12 | D�� | 18 |
16��ijһ����ϸ����ϸ������ϸ����֮��ľ���Ϊ0.0000075cm���ÿ�ѧ��������ʾΪ��������
| A�� | 7.5��106cm | B�� | 7.5��10-6cm | C�� | 7.5��10-5cm | D�� | -7.5��106cm |
 ��ͼ����A��B��C����С����B��A�ı�ƫ��85�㣬A����C�������Ϸ���B����C������ƫ��20�㷽�����ABC�Ķ�����
��ͼ����A��B��C����С����B��A�ı�ƫ��85�㣬A����C�������Ϸ���B����C������ƫ��20�㷽�����ABC�Ķ�����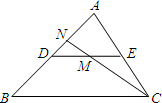 ��ͼ��DE�ǡ�ABC����λ�ߣ�M��DE���е㣬CM���ӳ��߽�AB�ڵ�N����S��DMN��S��DEA=1��6��
��ͼ��DE�ǡ�ABC����λ�ߣ�M��DE���е㣬CM���ӳ��߽�AB�ڵ�N����S��DMN��S��DEA=1��6��