Question

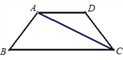
【题目】如图，将30°的直角三角尺ABC绕直角顶点A逆时针旋转到ADE的位置，使B点的对应点D落在BC边上，连接EB、EC，则下列结论：①∠DAC=∠DCA；②ED为AC的垂直平分线；③∠BED=30°；④ED=2AB．其中正确的是（　　）

A. ①②③ B. ①②④ C. ②③④ D. ①②③④

Answer 1

【答案】B

【解析】分析：先利用旋转的性质得到AB=AC，AC=AE，∠BAC=∠EAC，则可判断为等边三角形，所以则再计算出于是可对①进行判断；接着证明为等边三角形得到 加上，则根据线段垂直平分线的判定方法可对②进行判断；然后根据等边三角形的性质得DE平分∠AEC，则则可对③进行判断；接下来证明 则利用含的直角三角形三边的关系得到 所以 则可对④进行判断．

详解：在Rt△ABC中,∵∠ACB=

∴

∵△ABC绕直角顶点A逆时针旋转到ADE的位置，

∴AB=AC，AC=AE，∠BAC=∠EAC，

∴△ABD为等边三角形，

∴

∴

∵

∴

∴∠DAC=∠DCA，所以①正确；

∵

∴△AEC为等边三角形，

∴EA=EC，

而DA=DC，

∴ED为AC的垂直平分线，所以②正确；

∴DE平分∠AEC，

∴

∴ 所以③错误；

∵,

在Rt△AED中,∵

∴ED=2AD，

∴ED=2AB，所以④正确.

故选B.