题目内容
如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.(1)求证:直线AB是⊙O的切线;
(2)如果AC=1,BE=2,求⊙O的半径.

【答案】分析:(1)连接OE,证明△ACO≌△AEO,推出∠AEO=∠ACO=90°,根据切线的判定推出即可;
(2)求出AB、BC,证△BEO∽△BCA,得出比例式,代入求出即可.
解答:(1)证明:连接OE,
∵OD=OE,
∴∠ODE=∠OED,
∵DE∥AO,
∴∠COA=∠ODE,∠AOE=∠OED,
∴∠COA=∠AOE,
∵在△ACO和△AEO中

∴△ACO≌△AEO(SAS),
∴∠AEO=∠ACO,
∵AC⊥CD,
∴∠ACO=90°,
∴∠AEO=90°,
∵OE为半径,
∴直线AB是⊙O的切线.
(2)解:设⊙O的半径是R,
∵△ACO≌△AEO,
∴AC=AE=1,
∴AB=1+2=3,
在Rt△ACB中,由勾股定理得:BC= =2
=2 ,
,
∵∠BEO=90°=∠ACO,∠B=∠B,
∴△BEO∽△BCA,
∴ =
= ,
,
∴ =
= ,
,
R= ,
,
即⊙O的半径是 .
.
点评:本题考查了切线判定,全等三角形的性质和判定,相似三角形的性质和判定,等腰三角形的性质,平行线性质的应用,主要考查学生综合运用性质进行推理和计算的能力.
(2)求出AB、BC,证△BEO∽△BCA,得出比例式,代入求出即可.
解答:(1)证明:连接OE,

∵OD=OE,
∴∠ODE=∠OED,
∵DE∥AO,
∴∠COA=∠ODE,∠AOE=∠OED,
∴∠COA=∠AOE,
∵在△ACO和△AEO中

∴△ACO≌△AEO(SAS),
∴∠AEO=∠ACO,
∵AC⊥CD,
∴∠ACO=90°,
∴∠AEO=90°,
∵OE为半径,
∴直线AB是⊙O的切线.
(2)解:设⊙O的半径是R,
∵△ACO≌△AEO,
∴AC=AE=1,
∴AB=1+2=3,
在Rt△ACB中,由勾股定理得:BC=
 =2
=2 ,
,∵∠BEO=90°=∠ACO,∠B=∠B,
∴△BEO∽△BCA,
∴
 =
= ,
,∴
 =
= ,
,R=
 ,
,即⊙O的半径是
 .
.点评:本题考查了切线判定,全等三角形的性质和判定,相似三角形的性质和判定,等腰三角形的性质,平行线性质的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
相关题目
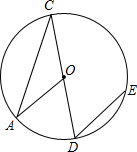 如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
如图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )| A、25° | B、30° | C、40° | D、50° |
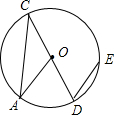 如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )
如图,已知CD是⊙O的直径,弦DE∥半径OA,∠D=50°,∠C=( )| A、50° | B、40° | C、25° | D、20° |
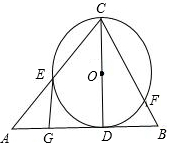 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.
如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O交CA于点E,点G是AD的中点.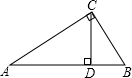 如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于
如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于 (2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.
(2012•苍梧县二模)如图,已知CD是⊙O的直径,AC⊥CD,垂足为C,弦DE∥OA,直线AE,CD相交于点B.