题目内容
 如图,△ABC的3个顶点都在⊙O上,AD是△ABC的高,AE是圆的直径,AB=
如图,△ABC的3个顶点都在⊙O上,AD是△ABC的高,AE是圆的直径,AB= ,AC=
,AC= ,AD=
,AD= ,则圆的半径是________.
,则圆的半径是________.
1.5
分析:设⊙O的半径为r,则AE=2r,由圆周角定理可知∠ACB=∠AEB,△ACD∽△AEB,利用相似三角形的对应边成比例即可求解.
解答:设⊙O的半径为r,则AE=2r,由圆周角定理可知∠ACB=∠AEB,
∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADE=90°,
∴△ACD∽△AEB,
∴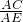 =
= ,
,
即 =
=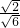 ,
,
解得r=1.5.
故答案为:1.5.
点评:本题考查的是圆周角定理及相似三角形的判定与性质,能判断出△ACD∽△AEB是解答此题的关键.
分析:设⊙O的半径为r,则AE=2r,由圆周角定理可知∠ACB=∠AEB,△ACD∽△AEB,利用相似三角形的对应边成比例即可求解.
解答:设⊙O的半径为r,则AE=2r,由圆周角定理可知∠ACB=∠AEB,
∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADE=90°,
∴△ACD∽△AEB,
∴
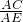 =
= ,
,即
 =
=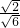 ,
,解得r=1.5.
故答案为:1.5.
点评:本题考查的是圆周角定理及相似三角形的判定与性质,能判断出△ACD∽△AEB是解答此题的关键.

练习册系列答案
相关题目
 18、如图,△ABC的三个内角大小分别为x,x,3x,则x的值为( )
18、如图,△ABC的三个内角大小分别为x,x,3x,则x的值为( ) 3、如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB的度数是( )
3、如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB的度数是( ) 如图,△ABC的三个顶点都在同一个圆上,∠BAC的平分线AE交BC于点D,交这个圆于点E.求证:BE2=ED•EA.
如图,△ABC的三个顶点都在同一个圆上,∠BAC的平分线AE交BC于点D,交这个圆于点E.求证:BE2=ED•EA. (2013•赣州模拟)如图,△ABC的三个顶点分别在正方形网格中的格点上.
(2013•赣州模拟)如图,△ABC的三个顶点分别在正方形网格中的格点上. (2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是
(2013•遂宁)如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是