题目内容
在数学中,为了简便,记 =1+2+3+…+(n﹣1)+n,
=1+2+3+…+(n﹣1)+n, =(x+1)+(x+2)+…+(x+n).
=(x+1)+(x+2)+…+(x+n).
(1)请你用以上记法表示:1+2+3+…+2011=_________;
(2)化简: ;
;
(3)化简: (x﹣k)(x﹣k﹣1)].
(x﹣k)(x﹣k﹣1)].
 =1+2+3+…+(n﹣1)+n,
=1+2+3+…+(n﹣1)+n, =(x+1)+(x+2)+…+(x+n).
=(x+1)+(x+2)+…+(x+n).(1)请你用以上记法表示:1+2+3+…+2011=_________;
(2)化简:
 ;
;(3)化简:
 (x﹣k)(x﹣k﹣1)].
(x﹣k)(x﹣k﹣1)].解:(1)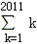 ;
;
(2)∵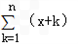 =(x+1)+(x+2)+…+(x+n),
=(x+1)+(x+2)+…+(x+n),
∴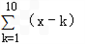 =(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10),
=(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10),
∴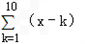 =(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10)
=(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10)
=10x﹣5×11
=10x﹣55;
(3)∵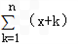 =(x+1)+(x+2)+…+(x+n),
=(x+1)+(x+2)+…+(x+n),
∴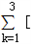 (x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4),
(x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4),
∴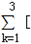 (x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4)
(x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4)
=(x﹣2)(2x﹣4)+(x﹣3)(x﹣4)
=(2x2﹣8x+8)+(x2﹣7x+12)
=2x2﹣8x+8+x2﹣7x+12
=3x2﹣15x+20.
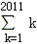 ;
;(2)∵
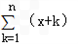 =(x+1)+(x+2)+…+(x+n),
=(x+1)+(x+2)+…+(x+n),∴
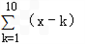 =(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10),
=(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10),∴
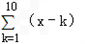 =(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10)
=(x﹣1)+(x﹣2)+(x﹣3)+…+(x﹣9)+(x﹣10)=10x﹣5×11
=10x﹣55;
(3)∵
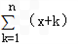 =(x+1)+(x+2)+…+(x+n),
=(x+1)+(x+2)+…+(x+n),∴
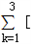 (x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4),
(x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4),∴
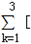 (x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4)
(x﹣k)(x﹣k﹣1)]=(x﹣1)(x﹣2)+(x﹣2)(x﹣3)+(x﹣3)(x﹣4)=(x﹣2)(2x﹣4)+(x﹣3)(x﹣4)
=(2x2﹣8x+8)+(x2﹣7x+12)
=2x2﹣8x+8+x2﹣7x+12
=3x2﹣15x+20.

练习册系列答案
相关题目
