题目内容
有二次根式:①
,②
,③
,④
,⑤
,⑥
,从中任意抽取一个,是最简二次根式的机会为( )
| 8 |
| x2+y2 |
| x2-y2 |
| x2y |
|
| 2 | ||
|
分析:判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答:解:①
=2
,被开方数含能开得尽方的因数,不是最简二次根式;
②
是最简二次根式;
③
是最简二次根式;
④
=|x|
,被开方数含能开得尽方的因式,不是最简二次根式;
⑤
=
,被开方数含分母,不是最简二次根式;
⑥
=
,被开方数含分母,不是最简二次根式;
综上所述,以上根式中的最简二次根式有2个,所以从中任意抽取一个,是最简二次根式的机会为:
=
.
故选B.
| 8 |
| 2 |
②
| x2+y2 |
③
| x2-y2 |
④
| x2y |
| y |
⑤
|
| ||
| 2 |
⑥
| 2 | ||
|
2
| ||
| 2 |
综上所述,以上根式中的最简二次根式有2个,所以从中任意抽取一个,是最简二次根式的机会为:
| 2 |
| 6 |
| 1 |
| 3 |
故选B.
点评:本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.
(1)被开方数不含分母;
(2)被开方数不含能开得尽方的因数或因式.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤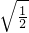 ,⑥
,⑥ ,
,



 ,②
,② ,③
,③ ,④
,④ ,⑤
,⑤ ,⑥
,⑥ ,从中任意抽取一个,是最简二次根式的机会为( )
,从中任意抽取一个,是最简二次根式的机会为( )


