题目内容
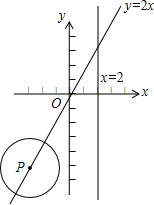（2013•温州二模）如图，P为正比例函数y=2x图象上的一个动点，⊙P的半径为2，圆心P从点（-3，-6），开始以每秒1个单位的速度沿着直线y=2x运动，当⊙P与直线x=2相切时，则该圆运动的时间为（ ）秒．分析：分两种情况：⊙P在直线x=2的左边和⊙P在直线x=2的右边两种情况．下面以第一种情况为例，分析一下解题思路：如图1，通过相似三角形：△AQ′P′∽△AQP，的对应边成比例得到比例式
=
，即
=
，从而求得AP′=2
，则易求PP′的长度．同理，当⊙P在直线x=2的右边时，可以求得PP′的另一长度．
| AP′ |
| AP |
| P′Q′ |
| PQ |
| AP′ | ||
5
|
| 2 |
| 5 |
| 5 |
解答：
解：设直线y=2x与x=2交于点A．则A（2，4）．
∵P（-3，-6），
∴AP=5
．
假设⊙P与直线x=2相切于点Q′，连接P′Q′．则P′Q′⊥AQ′．
过点P作PQ⊥AQ′于点Q．则P′Q′∥PQ．
∴△AQ′P′∽△AQP，
∴
=
，
=
，
解得AP′=2
，
①如图1，当⊙P在直线x=2的左边时．
PP′=AP-AP′=3
，
则该圆运动的时间为3
÷1=3
（秒）；
②如图2，当⊙P在直线x=2的右边时．
PP′=AP+AP′=7
，
则该圆运动的时间为7
÷1=7
（秒）；
综上所述，该圆运动的时间为3
秒或7
秒．
故选D．
解：设直线y=2x与x=2交于点A．则A（2，4）．∵P（-3，-6），
∴AP=5
| 5 |
假设⊙P与直线x=2相切于点Q′，连接P′Q′．则P′Q′⊥AQ′．
过点P作PQ⊥AQ′于点Q．则P′Q′∥PQ．
∴△AQ′P′∽△AQP，
∴
| AP′ |
| AP |
| P′Q′ |
| PQ |
| AP′ | ||
5
|
| 2 |
| 5 |
解得AP′=2
| 5 |
①如图1，当⊙P在直线x=2的左边时．
PP′=AP-AP′=3
| 5 |
则该圆运动的时间为3
| 5 |
| 5 |
②如图2，当⊙P在直线x=2的右边时．
PP′=AP+AP′=7
| 5 |
则该圆运动的时间为7
| 5 |
| 5 |
综上所述，该圆运动的时间为3
| 5 |
| 5 |
故选D．
点评：本题考查了一次函数综合题．解题时，主要利用了直线与圆相切时圆心与直线的距离关系，难度不大，难点在于要分⊙P在直线x=2的左边与右边两种情况进行讨论．
练习册系列答案
相关题目
（2013•温州二模）如图，圆锥的底面半径为3cm，高为4cm，那么这个圆锥的侧面积是
（2013•温州二模）如图是由5个大小相同的正方体组成的几何体，它的左视图是（ ）