题目内容
 (1997•陕西)如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是( )
(1997•陕西)如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是( )分析:延长AD到E,使AD=DE,连接BE,证△ADC≌△EDB,推出BE=AC,根据三角形三边关系定理推出即可.
解答:解:
延长AD到E,使AD=DE,连接BE,
∵AD是BC边上的中线,
∴BD=DC,
在△ADC和△EDB中
∴△ADC≌△EDB(SAS),
∴BE=AC,
在△ABE中,AB+BE>AE,
∵AD=DE,
∴AB+AC>2AD,
∴AD<
(AB+AC),
故选C.

延长AD到E,使AD=DE,连接BE,
∵AD是BC边上的中线,
∴BD=DC,
在△ADC和△EDB中
|
∴△ADC≌△EDB(SAS),
∴BE=AC,
在△ABE中,AB+BE>AE,
∵AD=DE,
∴AB+AC>2AD,
∴AD<
| 1 |
| 2 |
故选C.
点评:本题考查了全等三角形的性质和判定,三角形三边关系定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
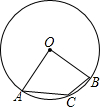 (1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( )
(1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( ) (1997•陕西)如图,已知△ABC内接于半径为r的半圆内,直径AB为其一边,设AC+BC=S,则有( )
(1997•陕西)如图,已知△ABC内接于半径为r的半圆内,直径AB为其一边,设AC+BC=S,则有( )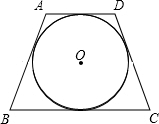 (1997•陕西)如图,四边形ABCD是⊙O的外切等腰梯形,其周长为20,则梯形ABCD的中位线长为
(1997•陕西)如图,四边形ABCD是⊙O的外切等腰梯形,其周长为20,则梯形ABCD的中位线长为 (1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=
(1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=