题目内容
 (1997•陕西)如图,已知△ABC内接于半径为r的半圆内,直径AB为其一边,设AC+BC=S,则有( )
(1997•陕西)如图,已知△ABC内接于半径为r的半圆内,直径AB为其一边,设AC+BC=S,则有( )分析:过C作CD⊥AB于D,在Rt△ACB中,得出AC2+BC2=AB2=(2r)2=4r2,AC×BC=2r×CD≤2R2,把AC+BC=S两边平方即可得出答案.
解答:解:
过C作CD⊥AB于D,
则CD≤r,
∵AB是直径,
∴∠ACB=90°,
∴AC2+BC2=AB2=(2r)2=4r2,
S△ACB=
×AC×BC=
×AB×CD,
AC×BC=2r×CD≤2R2,
∵AC+BC=S,
∴S2=(AC+BC)2=AC2+BC2+2AC×BC
=4r2+2AB×CD≤4r2+2r2,
即S2≤6r2,
故选C.

过C作CD⊥AB于D,
则CD≤r,
∵AB是直径,
∴∠ACB=90°,
∴AC2+BC2=AB2=(2r)2=4r2,
S△ACB=
| 1 |
| 2 |
| 1 |
| 2 |
AC×BC=2r×CD≤2R2,
∵AC+BC=S,
∴S2=(AC+BC)2=AC2+BC2+2AC×BC
=4r2+2AB×CD≤4r2+2r2,
即S2≤6r2,
故选C.
点评:本题考查了圆周角定理,勾股定理,三角形的面积等知识点的应用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
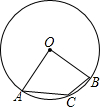 (1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( )
(1997•陕西)如图,已知在⊙O中,点A,B,C均在圆上,∠AOB=80°,则∠ACB等于( ) (1997•陕西)如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是( )
(1997•陕西)如图,已知在△ABC中,AD是BC边上的中线,则下列结论中正确的是( )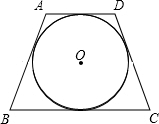 (1997•陕西)如图,四边形ABCD是⊙O的外切等腰梯形,其周长为20,则梯形ABCD的中位线长为
(1997•陕西)如图,四边形ABCD是⊙O的外切等腰梯形,其周长为20,则梯形ABCD的中位线长为 (1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=
(1997•陕西)如图,已知矩形ABCD中,AB=10,BC=12,E为DC的中点,AF⊥BE于点F,则AF=