��Ŀ����
����Ŀ����ѧ������ʦ������������⣺
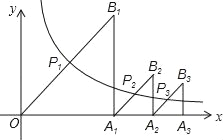
�߹���ͼ����![]() ��
��![]() ���ϵĸ���
���ϵĸ���
��֪��![]() ��
��
������![]() ��
��![]() ���ϵĸ���
���ϵĸ���![]() ��
��
������С����Ƶġ���![]() ��
��![]() ���ϵĸ��ߡ��ij߹���ͼ���̣�
���ϵĸ��ߡ��ij߹���ͼ���̣�
��������ͼ��
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶�������Ե�
�ij�Ϊ�뾶�������Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() �ij�Ϊ�뾶������������
�ij�Ϊ�뾶������������![]() �·����ڵ�
�·����ڵ�![]() ��
��
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
�����߶�![]() ��
��![]() ��
��![]() ���ϵĸ��ߣ�
���ϵĸ��ߣ�
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ���������ͼ�ۼ���
��2��С�ֺ�С������С����������֤����
С�֣�֤����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() �ֱ����߶�
�ֱ����߶�![]() �Ĵ�ֱƽ�����ϣ�����1����
�Ĵ�ֱƽ�����ϣ�����1����
![]() ��ֱƽ���߶�
��ֱƽ���߶�![]() ��
��
![]() �߶�
�߶�![]() ��
��![]() ��
��![]() ���ϵĸ��ߣ�
���ϵĸ��ߣ�
С�֣�֤����![]() ��
��![]() ��
��![]()
![]()
![]()
��![]()
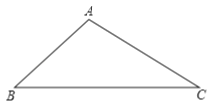
![]() ������2��
������2��
���߶�![]() ��
��![]() ��
��![]() ���ϵĸ���
���ϵĸ���
����֤�������еġ�����1���͡�����2���ֱ�ָʲô?
��3�������ò�ͬ��С���ķ��������ʦ��������⣮
��4����![]() ��
��![]() ��
��![]() ����
����![]() ���ϵĸ�
���ϵĸ�![]() �ij���Ϊ__________��
�ij���Ϊ__________��
���𰸡���1�������������2������1�����߶������˵������ȵĵ����߶εĴ�ֱƽ�����ϣ�����2�����ߺ�һ����3�������������4��![]()
��������
��1������Ҫ��ͼ�μ��ɣ�
��2�������߶εĴ�ֱƽ���ߵ��ж��͵��������ε����ʼ��ɽ������
��3�������ȹ���һ������������Ȼ�����ô�ֱƽ���ߵ��ж���������
��4������30����������ʼ����ɶ������������
�⣺��1��ͼ����ͼ��ʾ��
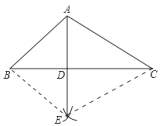
��2������1�����߶������˵������ȵĵ����߶εĴ�ֱƽ������
����2�����ߺ�һ
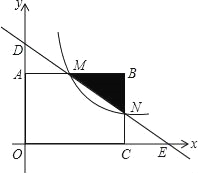
��3����ͼ��ʾ
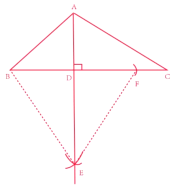
����![]() ΪԲ��
ΪԲ��![]() ��Ϊ�뾶��
��Ϊ�뾶��![]() �Ͻ�ȡ
�Ͻ�ȡ![]()
�������ⳤΪ�뾶�ֱ���![]() ��
��![]() ΪԲ�Ļ������ڵ�E
ΪԲ�Ļ������ڵ�E
������![]() ��
��![]() ��
��![]() ������
������
��4��![]()

 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�