题目内容
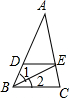如图，BE是△ABC中∠ABC的平分线．DE∥BC，若AE=3，AD=4，AC=5，求DE的长．
分析：先根据平行线的性质及角平分线的性质求出△BDE是等腰三角形，即BD=DE，再根据△ADE∽△ABC即可求出BD的长，进而求出DE的长．
解答：
解：∵BE是△ABC中∠ABC的平分线，DE∥BC，
∴∠1=∠2，∠2=∠3，∴∠1=∠3，
∴BD=DE，
∵DE∥BC，AE=3，AD=4，AC=5，
∴△ADE∽△ABC，
=
，
即
=
，
=
，解得BD=
．
∴DE=BD=
．
解：∵BE是△ABC中∠ABC的平分线，DE∥BC，∴∠1=∠2，∠2=∠3，∴∠1=∠3，
∴BD=DE，
∵DE∥BC，AE=3，AD=4，AC=5，
∴△ADE∽△ABC，
| AD |
| AB |
| AE |
| AC |
即
| AD |
| AD+BD |
| AE |
| AC |
| 4 |
| 4+BD |
| 3 |
| 5 |
| 8 |
| 3 |
∴DE=BD=
| 8 |
| 3 |
点评：本题难度一般，考查的是平行线的性质及相似三角形的性质．
练习册系列答案
相关题目
如图，BE是△ABC的外接⊙O的直径，CD是△ABC的高．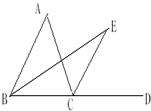
19、如图，BE是∠ABC的角平分线，AB∥CE，如果已知∠A=50°，∠E=30°，则∠ACD=
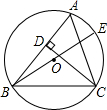已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高．
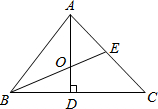如图，BE是△ABC的角平分线，AD是△ABC的高，∠ABC=60°，则∠AOE=