题目内容
如图,抛物线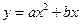 (a
(a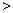 0)与双曲线
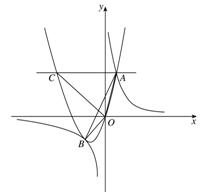
0)与双曲线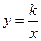 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).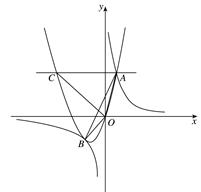
(1)求实数a,b,k的值;
(2)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.
le cellpadding="0" cellspacing="0">
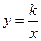 上,
上,
 所以k=4. 故双曲线的函数表达式为
所以k=4. 故双曲线的函数表达式为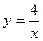 .
.
设点B(t,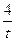 ),
),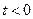 ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为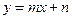 ,则有
,则有
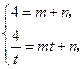 解得
解得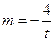 ,
, .
.
于是,直线AB与y轴的交点坐标为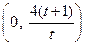 ,故
,故
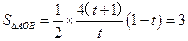 ,整理得
,整理得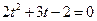 ,
,
解得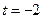 ,或t=
,或t=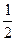 (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为(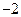 ,
,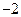 ).
).
因为点A,B都在抛物线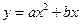 (a
(a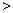 0)上,所以
0)上,所以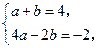 得
得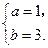 …………(10分)
…………(10分)
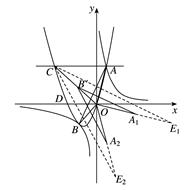
(2)如图,因为AC∥x轴,所以C(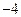 ,4),于是CO=4
,4),于是CO=4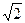 . 又BO=2
. 又BO=2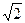 ,所以
,所以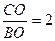 .
.
设抛物线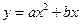 (a
(a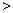 0)与x轴负半轴相交于点D, 则点D的坐标为(
0)与x轴负半轴相交于点D, 则点D的坐标为(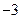 ,0).因为∠COD=∠BOD=
,0).因为∠COD=∠BOD=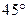 ,所以∠COB=
,所以∠COB=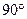 .
.
(i)将△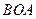 绕点O顺时针旋转
绕点O顺时针旋转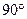 ,得到△
,得到△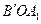 .这时,点
.这时,点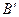 (
(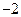 ,2)是CO的中点,点
,2)是CO的中点,点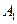 的坐标为(4,
的坐标为(4,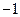 ).
).
延长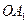 到点
到点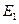 ,使得
,使得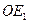 =
=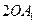 ,这时点
,这时点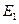 (8,
(8,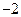 )是符合条件的点.
)是符合条件的点.
(ii)作△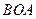 关于x轴的对称图形△
关于x轴的对称图形△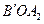 ,得到点
,得到点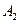 (1,
(1,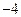 );延长
);延长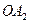 到点
到点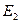 ,使得
,使得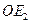 =
=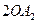 ,这时点E2(2,
,这时点E2(2,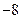 )是符合条件的点.
)是符合条件的点.
所以,点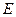 的坐标是(8,
的坐标是(8,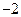 ),或(2,
),或(2,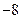 ). …………(20分)解析:
). …………(20分)解析:
略
(第12题) |
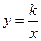 上,
上, 所以k=4. 故双曲线的函数表达式为
所以k=4. 故双曲线的函数表达式为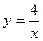 .
.设点B(t,
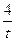 ),
),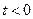 ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为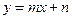 ,则有
,则有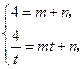 解得
解得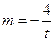 ,
, .
.于是,直线AB与y轴的交点坐标为
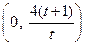 ,故
,故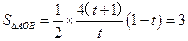 ,整理得
,整理得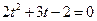 ,
,解得
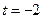 ,或t=
,或t=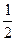 (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为(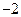 ,
,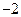 ).
).因为点A,B都在抛物线
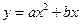 (a
(a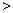 0)上,所以
0)上,所以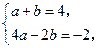 得
得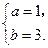 …………(10分)
…………(10分)(2)如图,因为AC∥x轴,所以C(
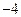 ,4),于是CO=4
,4),于是CO=4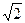 . 又BO=2
. 又BO=2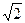 ,所以
,所以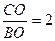 .
.
|
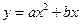 (a
(a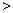 0)与x轴负半轴相交于点D, 则点D的坐标为(
0)与x轴负半轴相交于点D, 则点D的坐标为(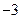 ,0).因为∠COD=∠BOD=
,0).因为∠COD=∠BOD=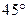 ,所以∠COB=
,所以∠COB=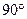 .
.(i)将△
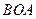 绕点O顺时针旋转
绕点O顺时针旋转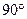 ,得到△
,得到△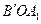 .这时,点
.这时,点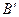 (
(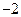 ,2)是CO的中点,点
,2)是CO的中点,点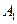 的坐标为(4,
的坐标为(4,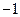 ).
).延长
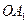 到点
到点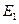 ,使得
,使得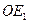 =
=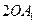 ,这时点
,这时点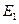 (8,
(8,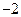 )是符合条件的点.
)是符合条件的点.(ii)作△
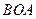 关于x轴的对称图形△
关于x轴的对称图形△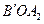 ,得到点
,得到点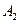 (1,
(1,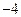 );延长
);延长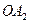 到点
到点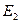 ,使得
,使得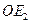 =
=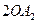 ,这时点E2(2,
,这时点E2(2,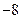 )是符合条件的点.
)是符合条件的点.所以,点
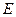 的坐标是(8,
的坐标是(8,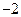 ),或(2,
),或(2,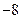 ). …………(20分)解析:
). …………(20分)解析:略

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
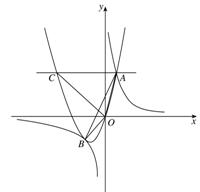
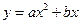 (a
(a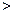 0)与反比例函数
0)与反比例函数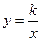 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)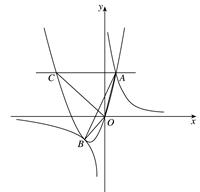
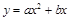 (a
(a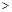 0)与双曲线
0)与双曲线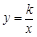 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).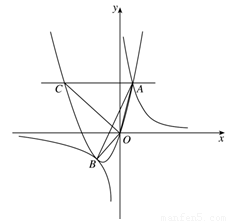
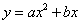 (a
(a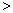 0)与反比例函数
0)与反比例函数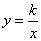 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)