题目内容
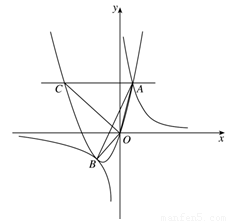
如图,抛物线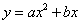 (a
(a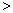 0)与反比例函数
0)与反比例函数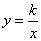 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
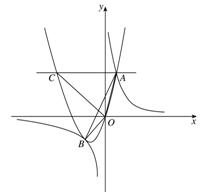
1.求反比例函数的解析式
2.用含t的代数式表示直线AB的解析式;
3.求抛物线的解析式;
4.过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
【答案】
1.因为点A(1,4)在反比例函数 上,
上,
所以k=4. 故反比例函数表达式为 . ………
. ………
2.设点B(t, ),
), ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为 ,则有
,则有
 解得
解得 ,
, .
.
直线AB的解析式为y= - x+ ………………………………………… 3分
3.直线AB与y轴的交点坐标为 ,故
,故
 ,整理得
,整理得 ,
,
解得 ,或t=
,或t= (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为( ,
, ).
).
因为点A,B都在抛物线 (a
(a 0)上,所以
0)上,所以 解得
解得
所以抛物线的解析式为y=x2+3x ……………… 4分
4.画出图形………………………………………………2分

点 的坐标是(8,
的坐标是(8, ),或(2,
),或(2, )………………
2分
)………………
2分
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
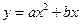 (a
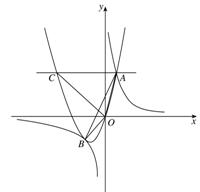
(a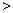 0)与双曲线
0)与双曲线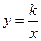 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).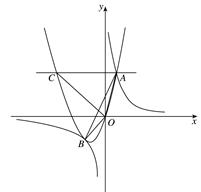
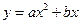 (a
(a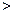 0)与反比例函数
0)与反比例函数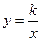 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点)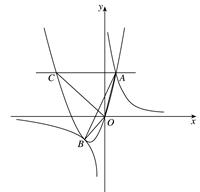
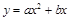 (a
(a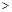 0)与双曲线
0)与双曲线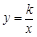 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).