题目内容
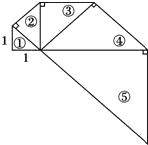 如图,第①个等腰直角三角形的直角边长等于1,以它的斜边长为腰长作第②个等腰直角三角形,再以第②个等腰直角三角形的斜边长为腰长作第③个等腰直角三角形….依次得到一系列的等腰直角三角形,其序号依次为①、②、③、④、….
如图,第①个等腰直角三角形的直角边长等于1,以它的斜边长为腰长作第②个等腰直角三角形,再以第②个等腰直角三角形的斜边长为腰长作第③个等腰直角三角形….依次得到一系列的等腰直角三角形,其序号依次为①、②、③、④、….(1)分别求出第①、②、③、④个等腰直角三角形的斜边长;
(2)归纳出第n个等腰直角三角形的斜边长.(n为正整数)
分析:(1)根据勾股定理分别计算;
(2)根据(1)中得到的数据,发现:第n个等腰直角三角形所对应的斜边正好是2的n次方的算术平方根.
(2)根据(1)中得到的数据,发现:第n个等腰直角三角形所对应的斜边正好是2的n次方的算术平方根.
解答:解:(1)第①个等腰直角三角形斜边长为
=
;
第②个等腰直角三角形的斜边长为
=2;
第③个等腰直角三角形的斜边长为
=2
;
第④个等腰直角三角形的斜边长为
=4.
(2)∵第①、②、③、④个等腰直角三角形的斜边长分别为(
)1=
,(
)2=2,
(
)3=2
,(
)4=4,故第n个等腰直角三角形的斜边长为(
)n.
| 12+12 |
| 2 |
第②个等腰直角三角形的斜边长为
(
|
第③个等腰直角三角形的斜边长为
| 22+22 |
| 2 |
第④个等腰直角三角形的斜边长为
(2
|
(2)∵第①、②、③、④个等腰直角三角形的斜边长分别为(
| 2 |
| 2 |
| 2 |
(
| 2 |
| 2 |
| 2 |
| 2 |
点评:能够熟练运用勾股定理,观察被开方数之间的联系.

练习册系列答案
相关题目
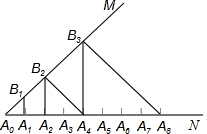 如图,∠MA0N=45°,A0A1=A1A2=A2A3=…=An-1An=1,按如图的方式作等腰直角三角形△A0B1A2、△A0B2A4、△A0B3A8…,则第n个等腰直角三角形的直角边长A0Bn=
如图,∠MA0N=45°,A0A1=A1A2=A2A3=…=An-1An=1,按如图的方式作等腰直角三角形△A0B1A2、△A0B2A4、△A0B3A8…,则第n个等腰直角三角形的直角边长A0Bn= 如图,直角三角形ADC是直角边长为1的等腰直角三角形,以直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,依此类推,第5个等腰直角三角形AFG的斜边AG长是
如图,直角三角形ADC是直角边长为1的等腰直角三角形,以直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,依此类推,第5个等腰直角三角形AFG的斜边AG长是 如图,第1个正方形(设边长为2)的边为第一个等腰直角三角形的斜边,第一个等腰直角三角形的直角边是第2个正方形的边,第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去.通过观察与研究,写出第2008个正方形的边长a2008为( )
如图,第1个正方形(设边长为2)的边为第一个等腰直角三角形的斜边,第一个等腰直角三角形的直角边是第2个正方形的边,第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去.通过观察与研究,写出第2008个正方形的边长a2008为( )