题目内容
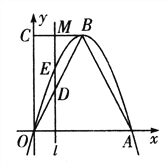
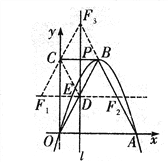
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB=
轴交于O点、A点,B为抛物线上一点,C为y轴上一点,连接BC,且BC//OA,已知点O(0,0),A(6,0),B(3,m),AB=![]() .
.
(1)求B点坐标及抛物线的解析式.,
(2)M是CB上一点,过点M作y轴的平行线交抛物线于点E,求DE的最大值;
(3)坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?若存在,求出符合条件的点F坐标;若不存在,请说明理由.

【答案】(1)B(6,0),y=![]() ;(2)
;(2)![]() ;(3) 满足条件的F点共3个:
;(3) 满足条件的F点共3个:![]() ,
,![]() ,
,![]()
【解析】分析:(1)运用勾股定理求出m的值,根据题意得点B为抛物线的顶点,设设抛物线为![]() ,即可求解;
,即可求解;
(2)可求![]() ,设E
,设E![]() ,则D(
,则D(![]() ,故DE=
,故DE=![]() ,从而可得结果;
,从而可得结果;
(3)设F![]() ,根据菱形的判定分三种情况进行讨论计算即可得解.
,根据菱形的判定分三种情况进行讨论计算即可得解.
详解:(1)如图,过点B作BG⊥OA于G,

由A(6,0),O(0,0)知抛物线对称轴为直线![]() ,
,
∴点B为抛物线的顶点。
∴AG=OG=3,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,
∴B(3,6),
设抛物线为![]() ,过点B(6,0),
,过点B(6,0),
∴9a+6=0
∴a=-![]() ,
,
∴y=-![]() (x-3)2+6=-
(x-3)2+6=-![]() x2+4x;
x2+4x;
(2)可求![]() ,设E
,设E![]() ,则D(
,则D(![]() ,
,
∴DE=![]() ,
,
∴当x=![]() ,DE最大=
,DE最大=![]() .
.
(3)设F![]() ,
,
![]()
①当CD为菱形对角线时,
∵FD∥BC,
∴![]()
∴
解得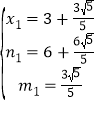 (舍去),
(舍去),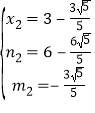 .
.
②当BD为菱形对角线时,![]()
∴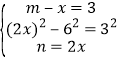
∴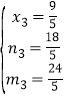 ,
,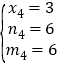 (舍去)
(舍去)
![]()
③当BC为菱形对角线时,D、F均在BC的垂直平分线上,且FP=PD,
则![]() ,则D(
,则D(![]() ,则PD=3,则
,则PD=3,则![]() ,
,![]() ,
,![]() 。
。
综上所述,满足条件的F点共3个:![]() ,
,![]() ,
,![]() 。
。

【题目】某学校计划组织全校1500名师生外出参加集体活动.经过研究,决定租用当地租车公司一共60辆![]() 、
、![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 400元 |
| 20人 | 300元 |
注:载客量指的是每辆客车最多可载该校师生的人数.
学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过22000元,一共有几种租车方案?并结合函数性质说明哪种租车方案最省钱?