题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 点,与
点,与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,且点
两点,且点![]() 在点
在点![]() 的右侧,设抛物线的顶点为
的右侧,设抛物线的顶点为![]() .
.
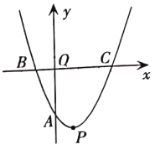
(1)若点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)当![]() 时,该抛物线上最高点与最低点纵坐标的差为
时,该抛物线上最高点与最低点纵坐标的差为![]() ,求出
,求出![]() 与
与![]() 的关系;若
的关系;若![]() 有最大值或最小值,直接写出这个最大值或最小值.
有最大值或最小值,直接写出这个最大值或最小值.
【答案】(1)2;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 有最小值,最小值为1.
有最小值,最小值为1.
【解析】
(1)由点B与点C关于直线x=1对称,可得出抛物线的对称轴为直线x=1,再利用二次函数的性质可求出b值;
(2)利用二次函数图象上点的坐标特征可求出点A的坐标,结合OA=OB可得出点B的坐标,由点B的坐标利用待定系数法可求出抛物线的解析式,由抛物线的解析式利用二次函数图象上点的坐标特征可求出点C的坐标,利用配方法可求出点P的坐标,再利用三角形的面积公式即可求出△BCP的面积;
(3)分b<-2,-2≤b≤0,0<b≤2,b>2四种情况考虑,利用二次函数图象上点的坐标特征结合二次函数的图象找出h关于b的关系式,再找出h的最值即可得出结论.
解:
(1)y=x(x-b)-![]() =x2-bx-
=x2-bx-![]() ,
,
∵点B与点C关于直线x=1对称,
∴![]() =1,
=1,
解得:b=2.
(2)当x=0时,y=x2-bx-![]() =-
=-![]() ,
,
∴点A的坐标为(0,-![]() ),
),
∴![]() ,
,
∵![]() ,
,
∴![]() 或
或![]() ,
,
当![]() 在
在![]() 上时,
上时,![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
当![]() 在
在![]() 上时,
上时,
∵![]() 点在
点在![]() 点右侧,
点右侧,
∴不符合题意.
综上所述可得![]() ,
,![]() .
.
此时抛物线![]() 的顶点纵坐标为
的顶点纵坐标为![]() .
.
∴![]() .
.
(3)抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,
①当![]() 即
即![]() 时,
时,
最高点纵坐标为![]() ,
,
最低点纵坐标为![]() ,
,
∴![]() ,当
,当![]() 时,
时,![]() .
.
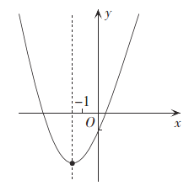
②当![]() 即
即![]() 时,
时,
最高点纵坐标为![]() ,
,
最低点纵坐标为![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 有最大值4,
有最大值4,
当![]() 时,
时,![]() 有最小值1.
有最小值1.
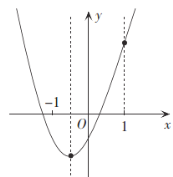
③当![]() 即
即![]() 时,
时,
最高点纵坐标为![]() ,
,
最低点纵坐标为![]() ,
,
∴![]() ,
,
当![]() 时
时![]() .
.
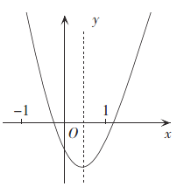
④当![]() 即
即![]() 时,
时,
最高点纵坐标为![]() ,
,
最低点纵坐标为![]() ,
,
∴![]() ,当
,当![]() ,即
,即![]() .
.
综上所述
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 有最小值,最小值为1.
有最小值,最小值为1.

 全能闯关100分系列答案
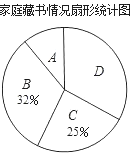
全能闯关100分系列答案【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.