题目内容
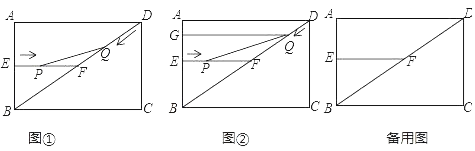
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
【答案】(1)证明见解析(2)![]() 或2(3)t=1或3或
或2(3)t=1或3或![]() 或
或![]() 秒时,△PQF是等腰三角形
秒时,△PQF是等腰三角形
【解析】试题分析:![]() 两组角对应相等,两三角形相似.
两组角对应相等,两三角形相似.
![]() 过点
过点![]() 作
作![]() 于
于![]() ,得出
,得出![]() 把
把![]() 用
用![]() 表示出来,即可表示出
表示出来,即可表示出![]() 的面积,求出
的面积,求出![]() 即可.
即可.
![]() 四边形
四边形![]() 为矩形时,
为矩形时,![]() 对应边的比相等,即可求出
对应边的比相等,即可求出![]() 得值.
得值.
![]() 分成四种情况进行讨论.
分成四种情况进行讨论.
试题解析:(1)∵四边形![]() 是矩形,
是矩形,
![]()
在![]() 中,
中,![]()
![]() 分别是
分别是![]() 的中点,
的中点,
![]()
![]()
![]()
![]()
(2)如图1,过点![]() 作
作![]() 于
于![]() ,
,

![]()
![]()
![]()
![]()
![]()
![]()
![]() (舍)或
(舍)或![]() 秒;
秒;
![]() 四边形
四边形![]() 为矩形时,如图所示:
为矩形时,如图所示:

![]()
![]()
![]()
解得:![]()
![]() 当点
当点![]() 在
在![]() 上时,如图2,
上时,如图2,![]()

![]()
![]()
当点![]() 在
在![]()
![]() 如图3,
如图3,

![]()
![]()
![]() 时,如图4,
时,如图4,

![]()
![]()
![]() 时,如图5,
时,如图5,

![]()
![]()
综上所述,![]() 或
或![]() 或
或![]() 或
或![]() 秒时,
秒时,![]() 是等腰三角形.
是等腰三角形.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】“十一”期间,某风景区在![]() 天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中每天游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化 单位:万人 |
|
|
|
|
|
| -1.2 |
(1)若![]() 月
月![]() 日的游客人数记为
日的游客人数记为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 月
月![]() 日的游客人数?
日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由.
(3)此风景区一方面给广大市民提供一个休闲游玩的好去处;另一方面拉动了内需,促进了消费.若![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,进园的人每人平均消费60元,问“十一”期间10月4日游园人员在此风景区的总消费是多少元?(用科学记数法表示)
万人,进园的人每人平均消费60元,问“十一”期间10月4日游园人员在此风景区的总消费是多少元?(用科学记数法表示)
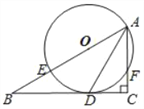
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
【题目】一次期中考试中,甲、乙、丙、丁、戍五位同学的数学、英语成绩等有关信息如下 表所示:(单位:分)
甲 | 乙 | 丙 | 丁 | 戍 | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择.标准分 的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.从标准分看, 标准分大的考试成绩更好.请问甲同学在本次考试中,数学与英语哪个学科考 得更好?