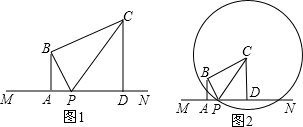
题目内容
(1)如图①,∠BAD的平分线AE与∠BCD的平分线CE交于点E,AB∥CD,∠ADC=40°,∠ABC=30°,求∠AEC的大小;
(2)如图②,∠BAD的平分线AE与∠BCD的平分线CE交于点E,∠ADC=m°,∠ABC=n°,求∠AEC的大小;
(3)如图③,∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间是否仍存在某种等量关系?若存在,请写出你得结论,并给出证明;若不存在,请说明理由.

(2)如图②,∠BAD的平分线AE与∠BCD的平分线CE交于点E,∠ADC=m°,∠ABC=n°,求∠AEC的大小;
(3)如图③,∠BAD的平分线AE与∠BCD的平分线CE交于点E,则∠AEC与∠ADC、∠ABC之间是否仍存在某种等量关系?若存在,请写出你得结论,并给出证明;若不存在,请说明理由.

分析:(1)由三角形内角和定理,可得∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,由角平分线的性质,可得∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,则可得∠E=
(∠D+∠B),继而求得答案;
(2)由三角形内角和定理,可得∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,由角平分线的性质,可得∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,则可得∠E=
(∠D+∠B),继而求得答案;
(3)首先延长BC交AD于点F,由三角形外角的性质,可得∠BCD=∠B+∠BAD+∠D,又由角平分线的性质,即可求得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由三角形内角和定理,可得∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,由角平分线的性质,可得∠ECD=∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)首先延长BC交AD于点F,由三角形外角的性质,可得∠BCD=∠B+∠BAD+∠D,又由角平分线的性质,即可求得答案.
解答:解:(1)∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E,
∴∠E=
(∠D+∠B),
∵∠ADC=40°,∠ABC=30°,
∴∠AEC=
×(40°+30°)=35°;
(2)∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E,
∴∠E=
(∠D+∠B),
∵∠ADC=m°,∠ABC=n°,
∴∠AEC=
;
(3)延长BC交AD于点F,
∵∠BFD=∠B+∠BAD,
∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D,
∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
∠BCD,∠EAD=∠EAB=
∠BAD,
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB-∠ECB=∠B+∠BAE-
∠BCD=∠B+∠BAE-
(∠B+∠BAD+∠D)=
(∠B-∠D),
即∠AEC=
.
∴∠ECD=∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB
∴∠D+∠B=2∠E,
∴∠E=
| 1 |
| 2 |
∵∠ADC=40°,∠ABC=30°,
∴∠AEC=
| 1 |
| 2 |
(2)∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠D+∠ECD=∠E+∠EAD,∠B+∠EAB=∠E+∠ECB,
∴∠D+∠ECD+∠B+∠EAB=∠E+∠EAD+∠E+∠ECB

∴∠D+∠B=2∠E,
∴∠E=
| 1 |
| 2 |
∵∠ADC=m°,∠ABC=n°,
∴∠AEC=
| m°+n° |
| 2 |
(3)延长BC交AD于点F,
∵∠BFD=∠B+∠BAD,
∴∠BCD=∠BFD+∠D=∠B+∠BAD+∠D,
∵CE平分∠BCD,AE平分∠BAD
∴∠ECD=∠ECB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠E+∠ECB=∠B+∠EAB,
∴∠E=∠B+∠EAB-∠ECB=∠B+∠BAE-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠AEC=
| ∠ABC-∠ADC |
| 2 |
点评:此题考查了三角形内角和定理、三角形外角的性质以及角平分线的定义.此题难度较大,注意掌握整体思想与数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、已知,如图,CA⊥BA于A,∠2+∠B=90°.
22、已知,如图,CA⊥BA于A,∠2+∠B=90°. 如图,射线BA,BC相交成90°角,O是射线BC上一点,以点O为圆心,
如图,射线BA,BC相交成90°角,O是射线BC上一点,以点O为圆心, 18、已知:如图,CD=BA,DF⊥BC,AE⊥BC,CE=BF.
18、已知:如图,CD=BA,DF⊥BC,AE⊥BC,CE=BF.