题目内容
在RtABC中，∠C=90°，AB=13，AC=12，BC=5，则下列各式中正确的是（ ）
分析：作出图形，然后根据锐角三角函数的定义对各选项分析判断后利用排除法求解．
解答：
解：如图，∵∠C=90°，AB=13，AC=12，BC=5，
∴A、sinA=
=
，故本选项错误；
B、cosA=
=
，故本选项正确；
C、tanA=
=
，故本选项错误；
D、tanA=
=
，故本选项错误．
故选B．
解：如图，∵∠C=90°，AB=13，AC=12，BC=5，∴A、sinA=
| BC |
| AB |
| 5 |
| 13 |
B、cosA=
| AC |
| AB |
| 12 |
| 13 |
C、tanA=
| BC |
| AC |
| 5 |
| 12 |
D、tanA=
| BC |
| AC |
| 5 |
| 12 |
故选B．
点评：本题考查锐角三角函数的定义，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
相关题目
在Rt
ABC中，
，D为边CA延长线上一点，DE//AB，
ADE=42
，则B的大小为
| A．42. | B．45. | C．48. | D．58. |
ABC中，
，D为边CA延长线上一点，DE//AB，
ADE=42
，则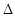
ABC中，∠C=90°,∠BAC=60°，AB=8.半径为
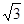的⊙M与射线BA相切，切点为N，且AN=3.将Rt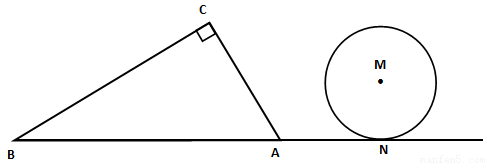
ABC中，∠C＝90°，两直角边AC、BC的长恰是方程
－4x＋2＝0的两个不同的根，则Rt
（B）
（D）2