题目内容
 如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AB的长是
如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=2,则AB的长是
- A.2
- B.4
- C.2

- D.4

C
分析:本题的关键是本题的关键是利用等边三角形和矩形对角线的性质即锐角三角函数关系求长度.
解答:∵在矩形ABCD中,AO= AC,DO=
AC,DO= BD,AC=BD,
BD,AC=BD,
∴AO=DO,
又∵∠AOD=60°,
∴∠ADB=60°,
∴∠ABD=30°,
∴ =tan30°,
=tan30°,
即 =
= ,
,
∴AB=2 .
.
故选C.
点评:本题考查了矩形的性质和锐角三角函数关系,具有一定的综合性,难度不大属于基础性题目.
分析:本题的关键是本题的关键是利用等边三角形和矩形对角线的性质即锐角三角函数关系求长度.
解答:∵在矩形ABCD中,AO=
 AC,DO=
AC,DO= BD,AC=BD,
BD,AC=BD,∴AO=DO,
又∵∠AOD=60°,
∴∠ADB=60°,
∴∠ABD=30°,
∴
 =tan30°,
=tan30°,即
 =
= ,
,∴AB=2
 .
.故选C.
点评:本题考查了矩形的性质和锐角三角函数关系,具有一定的综合性,难度不大属于基础性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
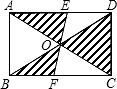 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为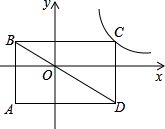 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线 (2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )
(2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( ) 如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=
如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=