Question

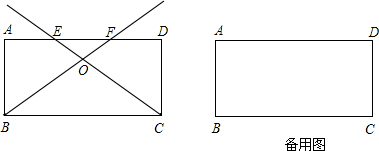
（2013•盐城模拟）如图，矩形ABCD中，AD=8，AB=4，点E沿A→D方向在线段AD上运动，点F沿D→A方向在线段DA上运动，点E、F速度都是每秒2个长度单位，E、F两点同时出发，且当E点运动到D点时两点都停止运动，设运动时间是t（秒）．
（1）当 0＜t＜2时，判断四边形BCFE的形状，并说明理由；
（2）当0＜t＜2时，射线BF、CE相交于点O，设S_△FEO=y，求y与t之间的函数关系式；
（3）问射线BF与射线CE所成的锐角是否能等于60°？若有可能，请求出t的值；若不能，请说明理由．

Answer 1

分析：（1）连结BE、CF，则AE=2t，DF=2t，易证得Rt△ABE≌Rt△DCF，得到BE=CF，由于EF∥BC，EF≠BC，所以可判断四边形BCFE为等腰梯形；
（2）过O点作MN⊥AD于M，交BC于N，由EF∥BC，根据三角形相似的判定方法得△OEF∽△OCB，则

OM

ON

=

EF

BC

，即

OM

4-OM

=

8-4t

8

，解得OM=

8-4t

4-t

，然后根据三角形面积公式可得到y与t的函数关系；
（3）讨论：当0＜t＜2时，∠ABE和∠DCF都小于45°，则△OBC为钝角三角形，则∠EOB=60°，所以∠OCB=∠OBC=30°，利用含30度的直角三角形三边的关系得到CH=

3

EH=4

3

，得到AE=8-4

3

，此时t=

8-4 3

2

=（4-2

3

）s；当2≤t≤4时，BF与CE相交于O点，∠BOC=60°，同理可得四边形BCEF为等腰梯形，则∠DOE=30°，得到ED=

CD

3

=

4 3

3

，则AE=8-

4 3

3

，利用速度公式得到此时t=

8- 4 3 3

2

=（4-

2

3

3

）s．

解答：解：（1）四边形BCFE为等腰梯形．理由如下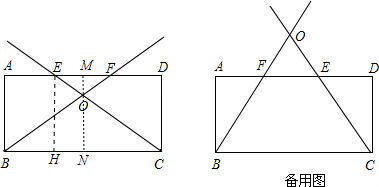
连结BE、CF，如图，
∵AE=2t，DF=2t，
∴AE=DF，
∵四边形ABCD为矩形，
∴AD∥BC，AB=CD，∠A=∠D=90°，
∴Rt△ABE≌Rt△DCF，
∴BE=CF，
而EF∥BC，EF≠BC，
∴四边形BCFE为等腰梯形；

（2）过O点作MN⊥AD于M，交BC于N，如图，
则MN⊥BC，
∴MN=AB=4，
则EF=8-2t-2t=8-4t，
∵EF∥BC，
∴△OEF∽△OCB，
∴

OM

ON

=

EF

BC

，即

OM

4-OM

=

8-4t

8

，解得OM=

8-4t

4-t

，
∴y=

1

2

OM•EF=

1

2

×

8-4t

4-t

×（8-4t），
即y=

4(4-2t)2

4-t

；

（3）存在．理由如下：
当0＜t＜2时，∠ABE和∠DCF都小于45°，则△OBC为钝角三角形，
若射线BF与射线CE所成的锐角等于60°，即∠EOB=60°，所以∠OCB=∠OBC=30°，
作EH⊥BC于H，则EH=4，
∴CH=

3

EH=4

3

，
∴BH=8-4

3

，
∴AE=8-4

3

，
∴t=

8-4 3

2

=（4-2

3

）s；
当2≤t≤4时，BF与CE相交于O点，如图，
若射线BF与射线CE所成的锐角等于60°，即∠BOC=60°，
同理可得四边形BCEF为等腰梯形，
∴∠OBC=∠OCB=60°，
∴∠DOE=30°，
∴ED=

CD

3

=

4 3

3

，
∴AE=8-

4 3

3

，
∴t=

8- 4 3 3

2

=（4-

2

3

3

）s．
∴当t=（4-2

3

）s或（4-

2

3

3

）s时，射线BF与射线CE所成的锐角等于60°．

点评：本题考查了四边形综合题：熟练掌握矩形的性质以及等腰梯形的判定；会运用三角形相似的性质和含30度的直角三角形三边的关系进行几何计算．