题目内容
 如图,⊙O为四边形ABCD内切圆,若∠AOB=70°,则∠COD的度数为度.
如图,⊙O为四边形ABCD内切圆,若∠AOB=70°,则∠COD的度数为度.
- A.100
- B.110
- C.120
- D.130
B
分析:连接OE,OF,OG,OH.根据切线长定理以及切线的性质,可以得到∠AOE=∠AOF,即可求得∠EOG的度数,进而求得∠COD的度数.
解答: 解:连接OE,OF,OG,OH.
解:连接OE,OF,OG,OH.
∵AD,AB是圆的切线,
∴∠DAO=∠BAO,
∴∠AOE=∠AOF,
同理:∠FOB=∠GOF,
∴∠EOG=2∠AOB=140°,
∴∠COD= (360°-∠EOG)=
(360°-∠EOG)= (360°-140°)=110°.
(360°-140°)=110°.
故选B.
点评:本题考查了切线长定理与切线的性质定理,正确证得:∠EOG=2∠AOB是关键.
分析:连接OE,OF,OG,OH.根据切线长定理以及切线的性质,可以得到∠AOE=∠AOF,即可求得∠EOG的度数,进而求得∠COD的度数.
解答:
 解:连接OE,OF,OG,OH.
解:连接OE,OF,OG,OH.∵AD,AB是圆的切线,
∴∠DAO=∠BAO,
∴∠AOE=∠AOF,
同理:∠FOB=∠GOF,
∴∠EOG=2∠AOB=140°,
∴∠COD=
 (360°-∠EOG)=
(360°-∠EOG)= (360°-140°)=110°.
(360°-140°)=110°.故选B.
点评:本题考查了切线长定理与切线的性质定理,正确证得:∠EOG=2∠AOB是关键.

练习册系列答案
相关题目
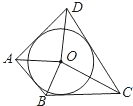 如图,⊙O为四边形ABCD内切圆,若∠AOB=70°,则∠COD的度数为( )度.
如图,⊙O为四边形ABCD内切圆,若∠AOB=70°,则∠COD的度数为( )度.| A、100 | B、110 | C、120 | D、130 |
 25、如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
25、如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB. 如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
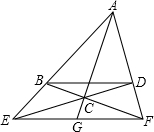 如图,ABCD为四边形,两组对边延长后得交点E、F,对角线BD∥EF,AC的延长线交EF于G.求证:EG=GF.
如图,ABCD为四边形,两组对边延长后得交点E、F,对角线BD∥EF,AC的延长线交EF于G.求证:EG=GF. 如图,⊙0为四边形ABCD的外接圆,AC为⊙0的直径,CD∥AB,点E、F分别在BC和AD上,且EF经过圆心0.
如图,⊙0为四边形ABCD的外接圆,AC为⊙0的直径,CD∥AB,点E、F分别在BC和AD上,且EF经过圆心0.