题目内容
 如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.(1)求证:AC平分∠DAB;
(2)若AC=8,
 |
| AC |
 |
| CD |
(3)若点B为
 |
| AC |
分析:(1)根据OC∥AB,可以得到∠OCA=∠CAB,在△OAC中,根据等角对等边,即可证明∠OAC=∠OCA,即可证得AC平分∠DAB;
(2)根据
:
=2:1,即可求得∠CAD的度数,在直角△ACD中,利用三角函数即可求得直径AD,进而求得半径;
(3)首先证明四边形是平行四边形,根据邻边相等,即可证得四边形是菱形.
(2)根据
 |
| AC |
 |
| CD |
(3)首先证明四边形是平行四边形,根据邻边相等,即可证得四边形是菱形.
解答:(1)证明:∵OC∥AB,
∴∠BAC=∠ACO,
∵OC=OA,
∴∠ACO=∠CAO.
∴∠CAO=∠BAC.
即:AC平分∠DAB.(2分)
(2)解:AC=8,弧AC与CD之比为2:1,
∴∠DAC=30°,
又∵AD是圆的直径,
∴∠ACD=90°
∴CD=AC•tan∠DAC=
,
∵∠COD=2∠DAC=60°,OD=OC,
∴△COD是等边三角形.
∴圆O的半径=CD=
(2分)
(3)解:∵点B为弧AC的中点,
∴
=
,
∴∠BAC=∠BCA,
∵AC平分∠DAB,
∴∠OAC=∠BAC,
∴∠BAC=∠BCA=∠OAC=∠OCA.
∴OA∥BC.又OC∥AB,
∴四边形ABCO是平行四边形.
∵AO=CO,
∴四边形ABCO为菱形.(3分)
∴∠BAC=∠ACO,
∵OC=OA,

∴∠ACO=∠CAO.
∴∠CAO=∠BAC.
即:AC平分∠DAB.(2分)
(2)解:AC=8,弧AC与CD之比为2:1,
∴∠DAC=30°,
又∵AD是圆的直径,
∴∠ACD=90°
∴CD=AC•tan∠DAC=
8
| ||
| 3 |
∵∠COD=2∠DAC=60°,OD=OC,
∴△COD是等边三角形.
∴圆O的半径=CD=
8
| ||
| 3 |
(3)解:∵点B为弧AC的中点,
∴
 |
| AB |
 |
| BC |
∴∠BAC=∠BCA,
∵AC平分∠DAB,
∴∠OAC=∠BAC,
∴∠BAC=∠BCA=∠OAC=∠OCA.
∴OA∥BC.又OC∥AB,
∴四边形ABCO是平行四边形.
∵AO=CO,
∴四边形ABCO为菱形.(3分)
点评:本题主要考查了圆的有关计算,根据弧的关系可以得到圆周角之间的关系,并且考查了菱形的判定定理.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
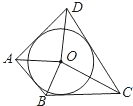 如图,⊙O为四边形ABCD内切圆,若∠AOB=70°,则∠COD的度数为( )度.
如图,⊙O为四边形ABCD内切圆,若∠AOB=70°,则∠COD的度数为( )度.| A、100 | B、110 | C、120 | D、130 |
 25、如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.
25、如图,⊙O为四边形ABCD的外接圆,圆心O在AD上,OC∥AB.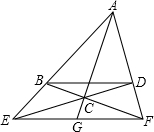 如图,ABCD为四边形,两组对边延长后得交点E、F,对角线BD∥EF,AC的延长线交EF于G.求证:EG=GF.
如图,ABCD为四边形,两组对边延长后得交点E、F,对角线BD∥EF,AC的延长线交EF于G.求证:EG=GF. 如图,⊙0为四边形ABCD的外接圆,AC为⊙0的直径,CD∥AB,点E、F分别在BC和AD上,且EF经过圆心0.
如图,⊙0为四边形ABCD的外接圆,AC为⊙0的直径,CD∥AB,点E、F分别在BC和AD上,且EF经过圆心0.