题目内容
在△ABC中,AM平分∠BAC交BC于M,AD是△ABC的高,且∠BAD=50°,∠DAC=20°,则∠MAC的度数为________.
15°
分析:根据题意画出图形,先根据∠BAD=50°,∠DAC=20°求出∠BAC的度数,再根据角平分线的定义求出∠CAM的度数,由∠MAC=∠CAM-∠DAC即可得出结论.
解答: 解:如图所示:AM平分∠BAC交BC于M,AD⊥BC于点D,
解:如图所示:AM平分∠BAC交BC于M,AD⊥BC于点D,
∵∠BAD=50°,∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°,
∵AM平分∠BAC交BC于M,
∴∠MAC= ∠BAC=
∠BAC= ×70°=35°,
×70°=35°,
∴∠MAC=∠CAM-∠DAC=35°-20°=15°.
故答案为:15°.
点评:本题考查的是三角形内角和定理、三角形的角平分线和高等知识,熟知三角形的内角和是180°是解答此题的关键.
分析:根据题意画出图形,先根据∠BAD=50°,∠DAC=20°求出∠BAC的度数,再根据角平分线的定义求出∠CAM的度数,由∠MAC=∠CAM-∠DAC即可得出结论.
解答:
 解:如图所示:AM平分∠BAC交BC于M,AD⊥BC于点D,
解:如图所示:AM平分∠BAC交BC于M,AD⊥BC于点D,∵∠BAD=50°,∠DAC=20°,
∴∠BAC=∠BAD+∠DAC=50°+20°=70°,
∵AM平分∠BAC交BC于M,
∴∠MAC=
 ∠BAC=
∠BAC= ×70°=35°,
×70°=35°,∴∠MAC=∠CAM-∠DAC=35°-20°=15°.
故答案为:15°.
点评:本题考查的是三角形内角和定理、三角形的角平分线和高等知识,熟知三角形的内角和是180°是解答此题的关键.

练习册系列答案
相关题目
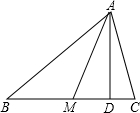 如图,在△ABC中,AM是中线,AD是高线.
如图,在△ABC中,AM是中线,AD是高线. 如图,在Rt△ABC中,AM平分∠ACB,CM=20cm,那么点M到直线AB的距离是
如图,在Rt△ABC中,AM平分∠ACB,CM=20cm,那么点M到直线AB的距离是 如图所示.在△ABC中,AM是BC边上的中线,AE平分∠BAC,BD⊥AE的延长线于D,且交AM延长线于F.求证:EF∥AB.
如图所示.在△ABC中,AM是BC边上的中线,AE平分∠BAC,BD⊥AE的延长线于D,且交AM延长线于F.求证:EF∥AB.