题目内容
菱形ABCD中，点P是对角线AC上的任意一点（不与A，C两点重合），以P为圆心的圆与AB相切，则AD与⊙P的位置关系是 ________．
相切
分析：根据菱形的对角线平分一组对角，以及角平分线上的点到角两边的距离相等，得点P到AD的距离等于点P到AB的距离．所以若以P为圆心的圆与AB相切，则AD与⊙P的位置关系是相切．
解答：∵点P到AD的距离等于点P到AB的距离，以P为圆心的圆与AB相切，
∴AD与⊙P的位置关系是相切．
故答案为：相切．
点评：本题综合运用了菱的性质和角平分线的性质，难度不大，关键是掌握菱形的对角线平分一组对角，以及角平分线上的点到角两边的距离相等．
分析：根据菱形的对角线平分一组对角，以及角平分线上的点到角两边的距离相等，得点P到AD的距离等于点P到AB的距离．所以若以P为圆心的圆与AB相切，则AD与⊙P的位置关系是相切．
解答：∵点P到AD的距离等于点P到AB的距离，以P为圆心的圆与AB相切，
∴AD与⊙P的位置关系是相切．
故答案为：相切．
点评：本题综合运用了菱的性质和角平分线的性质，难度不大，关键是掌握菱形的对角线平分一组对角，以及角平分线上的点到角两边的距离相等．
练习册系列答案
阅读快车系列答案
相关题目
16、（1）如图，在菱形ABCD中，点E是AB上的一点，连接DE交AC于点O，连接BO，且∠AED=50°，则∠CBO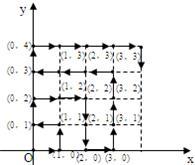
如图，菱形ABCD中，点B、D的坐标分别为（0，-1）和（0，3），A点的横坐标为-3，则过C点的反比例函数的解析式为
（2012•保定二模）如图所示，在菱形ABCD中，点E，F分别为AB，AC的中点，菱形ABCD的周长为32，则EF的长等于（ ）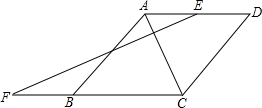
如图菱形ABCD中，点E是AD的中点，EF⊥AC交CB的延长线于点F，交AC于点M，想一想：AB与EF是否互相平分，并说明理由．
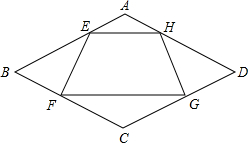如图，菱形ABCD中，点E，F，G，H分别在AB，BC，CD，DA上，且AE=AH=BF=DG=x，设四边形EFGH的面积为S．