Question

【题目】如图，在直角坐标平面中，O为原点，点A的坐标为（20，0），点B在第一象限内，BO＝10，sin∠BOA＝ ．

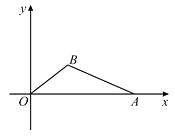
（1）在图中，求作△ABO的外接圆；（尺规作图，不写作法但需保留作图痕迹）
（2）求点B的坐标与cos∠BAO的值；
（3）若A，O位置不变，将点B沿 轴正半轴方向平移使得△ABO为等腰三角形，请直接写出平移距离．

Answer 1

【答案】
（1）

如图，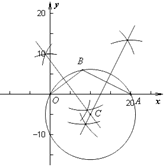

⊙C即为所求作的圆

（2）

B(8，6)

cos =

（3）

点B沿 轴向右平移2个单位或 或 个单位

【解析】（1）如图，分别作OB，OA的垂直平分线，得到它们的交点，再画圆，详细方法：
画OB的垂直平分线：分别以O，B为圆心，以大于OB的长度画弧，在OB的两侧相交于两点，连接它们，即是OB的垂直平分线；
画AB的垂直平分线：分别以A，B为圆心，以大于AB的长度画弧，在OB的两侧相交于两点，连接它们，即是AB的垂直平分线；
得到交点C，即是外接圆的圆心，以ＯＣ为半径画圆.

(2)如图1，过点B作BDOA于D，则在RtOBD中，sin∠BOA= ， BO=10，
则BD=OB×sin∠BOA=10×=6，
则OD=.
则B(8,6).
在RtABD中，因为A（20,0），则OA=20，AD=OA-OD=20-8=12，AB= ，
则cos ∠ BAO=.

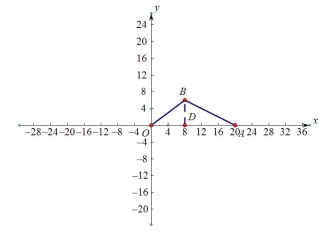
图1
(3)以OA为底时，如图2，OB=AB，则B（10,6），向x轴正方向平移了10-8=2；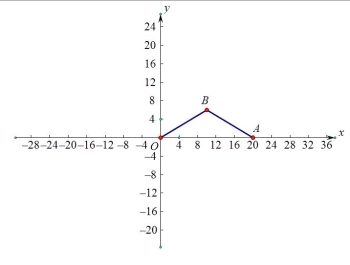

图2
以OB为底边时，如图3，AB=OA=20，则AD=,
则OD=OA-AD或OA+AD，即OD=或,
所以向x轴正半轴移动了18<0，不符合，合去，或；

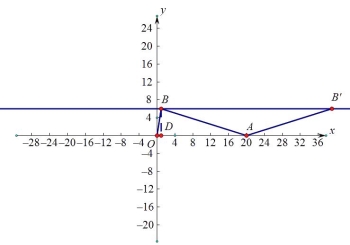
图3
以AB为底时，如图4，OB=OA=20，则OD=,
所以向x轴正半轴移动了.
综上，答案为：点B沿 轴向右平移2个单位或或个单位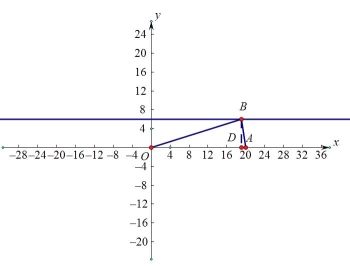

图4

【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对三角形的外接圆与外心的理解，了解过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心．