题目内容
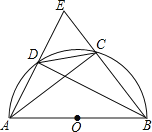
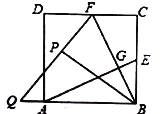
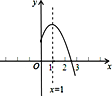
【题目】如图是二次函数![]() (a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2 ,0)和(3 ,0)之间,对称轴是x=1.对于下列结论:① ab<0;② 2a+b=0;③ 3a+c>0;④a+b≥m(am+b)(m为实数);⑤ 当-1<x<3时,y>0. 其中正确结论的个数为( )
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴判定b与0的关系以及2a+b=0;当x=-1时,y=a-b+c;然后由图象确定当x取何值时,y>0.
①∵对称轴在y轴右侧,
∴a、b异号,
∴ab<0,故正确;
②∵对称轴x=-![]() =1,
=1,
∴2a+b=0;故正确;
③∵2a+b=0,
∴b=-2a,
∵当x=-1时,y=a-b+c<0,
∴a-(-2a)+c=3a+c<0,故错误;
④根据图示知,当m=1时,有最大值;
当m≠1时,有am2+bm+c≤a+b+c,
所以a+b≥m(am+b)(m为实数).
故正确.
⑤如图,当-1<x<3时,y不只是大于0.
故错误.
故选:B.

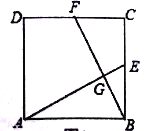
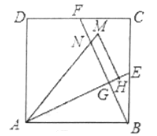
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在
在![]() 轴上,
轴上,![]() 是
是![]() 的中点,过点
的中点,过点![]() 的反比例函数图象交
的反比例函数图象交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() .
.
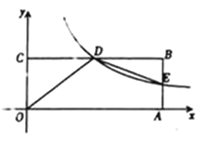
![]() 求过点
求过点![]() 的反比例函数的解析式及
的反比例函数的解析式及![]() 所在直线的函数解析式.
所在直线的函数解析式.
![]() 设直线
设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,求
,求![]() 的面积.
的面积.
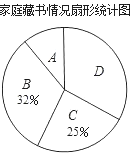
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.