题目内容
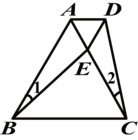 6.如图所示,△ABC是等边三角形,点E是AC上一点,∠
6.如图所示,△ABC是等边三角形,点E是AC上一点,∠
分析:由△ABC是等边三角形,即可得AB=AC,∠BAC=60°,又由∠1=∠2,BE=CD,即可根据SAS判定△ABE≌△ACD,即可得AD=AE,∠CAD=∠BAE=60°,然后由有一个角是60°的等腰三角形是等边三角形,即可判定△ADE是等边三角形.
解答:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
在△ABE和△ACD中,
| AB=AC ∠1=∠2 BE=CD |
∴△ABE≌△ACB(SAS),
∴AD=AE,∠CAD=∠BAE=60°,
∴△ADE是等边三角形.
点评:此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

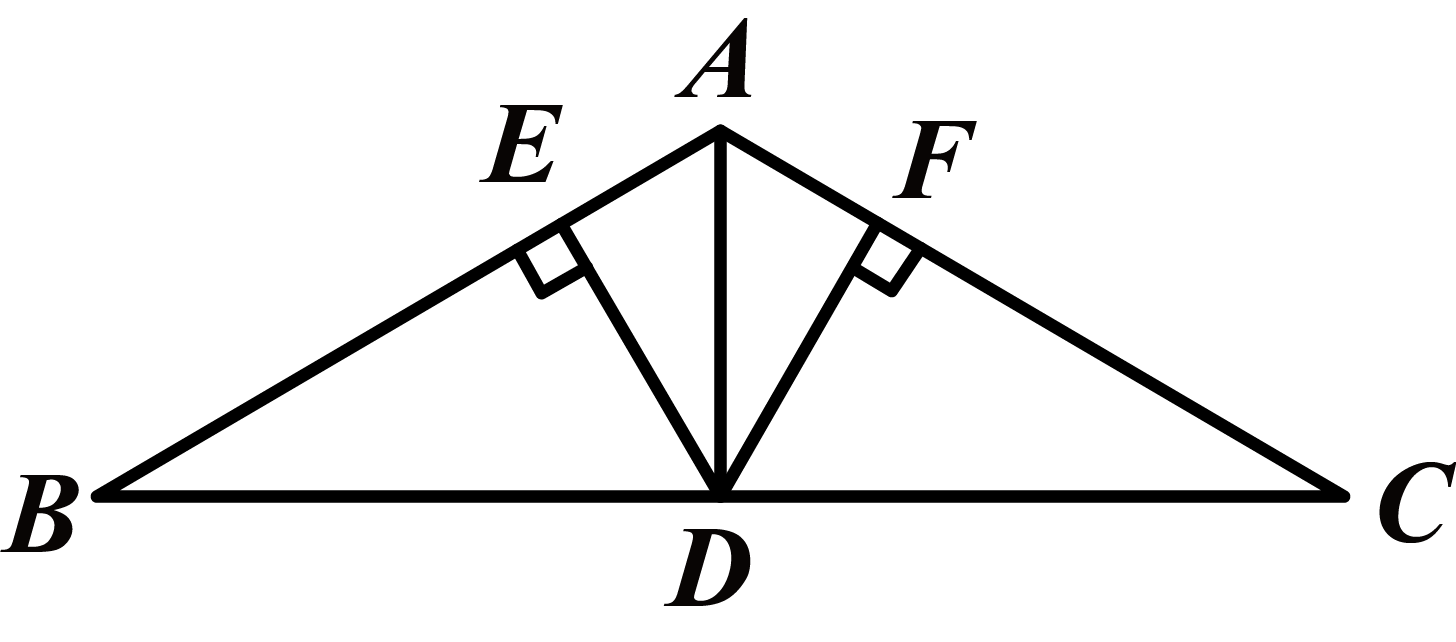 3.如图所示的是屋顶的“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10 m,AD为柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=________.
3.如图所示的是屋顶的“人字形”钢架,其中斜梁AB=AC,顶角∠BAC=120°,跨度BC=10 m,AD为柱(即底边BC的中线),两根支撑架DE⊥AB,DF⊥AC,则DE+DF=________.