题目内容
如图，ABCD，BEFC是两个全等的正方形，则tan（∠BAF+∠AFB）等于________．
1
分析：根据三角形内角与外角的关系求出∠BAF+∠AFB=∠FBE，再在△FBE中利用特殊角的三角函数值解答．
解答：∵∠FBE是△ABF的一个外角，
∴∠BAF+∠AFB=∠FBE，
∴tan（∠BAF+∠AFB）=tan∠FBE=
=1．
故答案为1．
点评：本题考查了三角函数的定义，利用三角形内角与外角的关系，将tan（∠BAF+∠AFB）转化tan∠FBE是解题的关键．
分析：根据三角形内角与外角的关系求出∠BAF+∠AFB=∠FBE，再在△FBE中利用特殊角的三角函数值解答．
解答：∵∠FBE是△ABF的一个外角，
∴∠BAF+∠AFB=∠FBE，
∴tan（∠BAF+∠AFB）=tan∠FBE=
=1．故答案为1．
点评：本题考查了三角函数的定义，利用三角形内角与外角的关系，将tan（∠BAF+∠AFB）转化tan∠FBE是解题的关键．
练习册系列答案
轻松暑假总复习系列答案
相关题目
如图矩形ABCD中，过A，B两点的⊙O切CD于E，交BC于F，AH⊥BE于H，连接EF．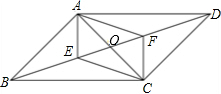
如图，?ABCD中，E是CD延长线上一点，BE与AD交于点F，DE=
（2012•武进区模拟）如图，?ABCD中，E是AD边的中点，BE的延长线与CD的延长线相交于F．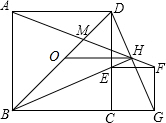
（2013•莘县二模）如图，ABCD、CEFG是正方形，E在CD上且BE平分∠DBC，O是BD中点，直线BE、DG交于H．BD，AH交于M，连接OH，下列四个结论：