Question

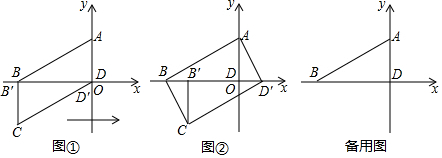
5．已知等腰△ABC中，AB=AC，AD∥BC，CD⊥AC，连接BD交AC于点P，
（1）如图1，若AB=5，BC=6，求$\frac{AP}{CP}$的值；
（2）如图2，过点C作CH⊥AB于点H，CH与BD交于点E，求证：CE=HE．

Answer 1

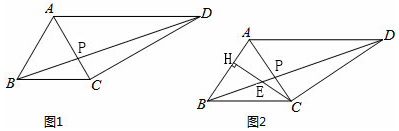
分析 （1）如图1，过A作AE⊥BC于E，根据等腰三角形的性质得到BE=CE=3，根据勾股定理得到AE=4，根据相似三角形的性质得到AD=$\frac{25}{3}$，即可得到结论；
（2）作CQ∥AB于Q，根据平行线分线段成比例定理得到$\frac{CQ}{AB}$=$\frac{BC}{AD}$，$\frac{CE}{HE}$=$\frac{CQ}{BH}$，$\frac{CQ}{AB}$=$\frac{BC}{AD}$，根据等腰三角形的性质得到∠ABC=∠ACB，根据相似三角形的性质得到$\frac{BH}{AC}$=$\frac{BC}{AD}$，于是得到$\frac{CQ}{AB}$=$\frac{BH}{AC}$，即可得到结论．

解答 解：（1）如图1，过A作AE⊥BC于E，
∵AB=AC=5，BC=6，
∴BE=CE=3，
∴AE=4，
∵AD∥BC，
∴AE⊥AD，
∴∠EAC+∠DAC=90°，
∵AC⊥CD，
∴∠CAD+∠ADC=90°，
∴∠EAC=∠ADC，
∴△ACE∽△DAC，
∴$\frac{AC}{AD}=\frac{CE}{AC}$，
∴AD=$\frac{25}{3}$，
∵AD∥BC，
∴△APD∽△CPB，
∴$\frac{AP}{PC}=\frac{AD}{BC}$=$\frac{25}{18}$；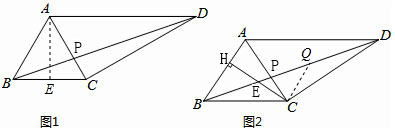
（2）证明：作CQ∥AB于Q，
如图所示：则$\frac{CQ}{AB}$=$\frac{BC}{AD}$，$\frac{CE}{HE}$=$\frac{CQ}{BH}$，
∵AD∥BC，
∴$\frac{CP}{AP}$=$\frac{BC}{AD}$，∠ACB=∠DAC，
∴$\frac{CQ}{AB}$=$\frac{BC}{AD}$，
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABC=∠DAC，
∵CH⊥AB，
∴∠BHC=90°=∠ACD，
∴△CHB∽△DCA，
∴$\frac{BH}{AC}$=$\frac{BC}{AD}$，
∴$\frac{CQ}{AB}$=$\frac{BH}{AC}$，
∴CQ=BH，
∴$\frac{CE}{HE}$═1，
∴CE=HE．

点评 本题考查了等边三角形的判定与性质、相似三角形的判定与性质、等边三角形的性质、正确的作出辅助线是解题的关键．