题目内容
利用公式法解方程:x2-x-3=0.
解:x2-x-3=0,
∵a=1,b=-1,c=-3,
∴△=(-1)2-4×1×(-3)=13>0,
∴x= =
=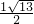 ,
,
∴x1=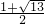 ,x2=
,x2=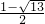 .
.
分析:观察方程为一般形式,找出此时二次项系数,一次项系数及常数项,计算出根的判别式,发现其结果大于0,故利用求根公式可得出方程的两个解.
点评:此题考查了利用公式法来求一元二次方程的解,利用此方法解方程时,首先将方程化为一般形式,找出相应的a,b及c的值,代入b2-4ac中求值,当b2-4ac≥0时,可代入求根公式来求解.
∵a=1,b=-1,c=-3,
∴△=(-1)2-4×1×(-3)=13>0,
∴x=
 =
=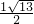 ,
,∴x1=
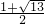 ,x2=
,x2=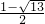 .
.分析:观察方程为一般形式,找出此时二次项系数,一次项系数及常数项,计算出根的判别式,发现其结果大于0,故利用求根公式可得出方程的两个解.
点评:此题考查了利用公式法来求一元二次方程的解,利用此方法解方程时,首先将方程化为一般形式,找出相应的a,b及c的值,代入b2-4ac中求值,当b2-4ac≥0时,可代入求根公式来求解.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目