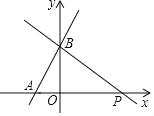
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l�ǵ�һ�������Ľ�ƽ���ߣ�
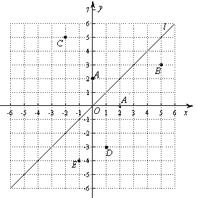
ʵ����̽����
��1����ͼ�۲���֪A��0��2������ֱ��l�ĶԳƵ�A��������Ϊ��2��0��������ͼ�зֱ����B��5��3����C����2��5������ֱ��l�ĶԳƵ�B����C����λ�ã���д�����ǵ����꣺B��_______��C��_______��
�����뷢�֣�
��2�����ͼ�ι۲��������������꣬��ᷢ�֣�����ƽ������һ��P��a��b�����ڵ�һ�������Ľ�ƽ����l�ĶԳƵ�P��������Ϊ________��
��������չ��
��3��ͼ����ֱ��l��ȡһ��Q��ʹQ��D��1��-3����E��-1��-4������ľ���֮����С�����Q��������____________��
���𰸡���1��![]() ����2����b��a������3��(
����2����b��a������3��(![]() )
)
��������
��1�����ҵ���![]() ���ڵ�һ��������ƽ���ߵĶԳƵ�
���ڵ�һ��������ƽ���ߵĶԳƵ�![]() ������Ϊ
������Ϊ![]() ���ٽ����֪�ĵ�
���ٽ����֪�ĵ�![]() �����꣬���Dz��Ѳ����C��������
�����꣬���Dz��Ѳ����C��������![]() ��
��
��2�����Է���![]() ����һ��������ƽ���ߴ�ֱ��ƽ�֣��ɴ˿������뵽����ƽ������һ��
����һ��������ƽ���ߴ�ֱ��ƽ�֣��ɴ˿������뵽����ƽ������һ��![]() ���ڵ�һ�������Ľ�ƽ����
���ڵ�һ�������Ľ�ƽ����![]() �ĶԳƵ�
�ĶԳƵ�![]() ������Ϊ(
������Ϊ(![]() ���������ݡ������껥��λ�ã�
���������ݡ������껥��λ�ã�
��3���ɣ�2���ã�D��1����3������ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ������Ϊ����3��1��������
������Ϊ����3��1��������![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����ʱ��
����ʱ��![]() ��
��![]() ����ľ���֮����С��
����ľ���֮����С��
��1����ͼ��ͨ���۲�֪![]() ��
��
��2����(1) �������뵽����ƽ������һ��![]() ���ڵ�һ�������Ľ�ƽ����
���ڵ�һ�������Ľ�ƽ����![]() �ĶԳƵ�
�ĶԳƵ�![]() ������Ϊ(
������Ϊ(![]() ���������ݡ������껥��λ�ã�
���������ݡ������껥��λ�ã�
���ǣ���b��a����
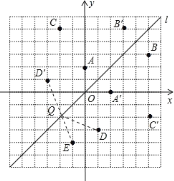
��3���ɣ�2���ã�![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ������Ϊ��-3��1��������
������Ϊ��-3��1��������![]() ��ֱ��
��ֱ��![]() �ڵ�
�ڵ�![]() ����ʱ��
����ʱ��![]() ��
��![]() ����ľ���֮����С��
����ľ���֮����С��
���D�䣨-3��1����E��-1��-4��ֱ�ߵĽ���ʽΪ![]() ��
��
��![]()
��
��ֱ��D��E�Ľ���ʽΪ��![]()
��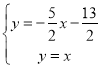
��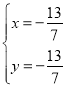
������Q�������Ϊ(![]() )��
)��