题目内容
 如图,O是直线AB上的一点,OD是∠BOC的平分线,OE是∠AOC平分线,则下列说法中错误的是
如图,O是直线AB上的一点,OD是∠BOC的平分线,OE是∠AOC平分线,则下列说法中错误的是
- A.∠COE与∠BOE互补
- B.∠EOC与∠BOD互余
- C.∠COD与∠AOD互补
- D.∠COD与∠BOD互余
D
分析:根据角平分线的性质,可得∠AOE=∠COE,∠COD=∠BOD,再根据余角和补角的定义求解即可.
解答:∵OD是∠BOC的平分线,OE是∠AOC平分线,
∴∠AOE=∠COE= ∠AOC,∠COD=∠BOD=
∠AOC,∠COD=∠BOD= ∠BOC,
∠BOC,
∵∠AOC+∠COB=180°,
∴∠COE+∠COD=90°,
A、∠COE与∠BOE互补,正确;
B、∠EOC与∠BOD互余,正确;
C、∠COD与∠AOD互补,正确
D、∠COD与∠BOD互余,错误;
故选D.
点评:本题考查了余角和补角的知识,解答本题的关键是理解余角和补角的定义,掌握角平分线的性质.
分析:根据角平分线的性质,可得∠AOE=∠COE,∠COD=∠BOD,再根据余角和补角的定义求解即可.
解答:∵OD是∠BOC的平分线,OE是∠AOC平分线,
∴∠AOE=∠COE=
 ∠AOC,∠COD=∠BOD=
∠AOC,∠COD=∠BOD= ∠BOC,
∠BOC,∵∠AOC+∠COB=180°,
∴∠COE+∠COD=90°,
A、∠COE与∠BOE互补,正确;
B、∠EOC与∠BOD互余,正确;
C、∠COD与∠AOD互补,正确
D、∠COD与∠BOD互余,错误;
故选D.
点评:本题考查了余角和补角的知识,解答本题的关键是理解余角和补角的定义,掌握角平分线的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
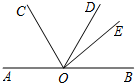 如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
 如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数.
如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数. 如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是
如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是 如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题:
如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题: