题目内容
图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是
- A.ab
- B.（a+b）2
- C.（a-b）2
- D.a2-b2
C
分析：中间部分的四边形是正方形，表示出边长，则面积可以求得．
解答：中间部分的四边形是正方形，边长是a+b-2b=a-b，
则面积是（a-b）2．
故选C．
点评：本题考查了列代数式，正确表示出小正方形的边长是关键．
分析：中间部分的四边形是正方形，表示出边长，则面积可以求得．
解答：中间部分的四边形是正方形，边长是a+b-2b=a-b，
则面积是（a-b）2．
故选C．
点评：本题考查了列代数式，正确表示出小正方形的边长是关键．
练习册系列答案
阅读快车系列答案
相关题目
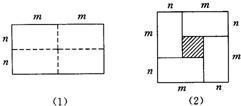
（2013•枣庄）图（1）是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（ ）
图（1）是一个长为2m，宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是
（1）图（1）是一个长为2m，宽为2他的矩形，把此矩形沿图中虚线用剪刀均分为四个小长方形，然后按图（2）的形状拼成一个大正方形．请问：这两个图形的什么量不变？