题目内容
已知:x=1- ,又y=1-
,又y=1- ,则用z表示x的代数式为________.
,则用z表示x的代数式为________.
x=
分析:先用x表示y= ,再把y代入y=1-
,再把y代入y=1- 得
得 =1-
=1- ,化简即可.
,化简即可.
解答:∵x=1- ,
,
∴y= ,
,
∴把y代入y=1- 得,
得, =1-
=1- ,
,
∴化简得x= .
.
点评:主要考查了等式的基本性质.
等式性质:
1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

分析:先用x表示y=
 ,再把y代入y=1-
,再把y代入y=1- 得
得 =1-
=1- ,化简即可.
,化简即可.解答:∵x=1-
 ,
,∴y=
 ,
,∴把y代入y=1-
 得,
得, =1-
=1- ,
,∴化简得x=
 .
.点评:主要考查了等式的基本性质.
等式性质:
1、等式的两边同时加上或减去同一个数或字母,等式仍成立;
2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

练习册系列答案
相关题目
 23、看图填空:
23、看图填空: 把下列推理过程补充完整.
把下列推理过程补充完整.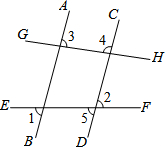 已知:如图,直线AB,CD被直线EF,GH所截,且∠1=∠2.
已知:如图,直线AB,CD被直线EF,GH所截,且∠1=∠2.