题目内容
把下列推理过程补充完整．已知：EF∥AD，∠1=∠2，试说明AB∥DG．
推理如下：∵EF∥AD（已知）
∴∠2=
∠3
∠3
又∵∠1=∠2（已知）
∴∠1=∠3
等量代换
等量代换
∴AB∥
DG
DG
．分析：根据平行线的性质由EF∥AD得∠2=∠3，而∠1=∠2，则∠1=∠3，然后根据平行线的判定即可得到AB∥DG．
解答：解：∵EF∥AD，
∴∠2=∠3，
又∵∠1=∠2，
∴∠1=∠3，
∴AB∥DG．
故答案为∠3，等量代换，DG．
∴∠2=∠3，
又∵∠1=∠2，
∴∠1=∠3，
∴AB∥DG．
故答案为∠3，等量代换，DG．
点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等．
练习册系列答案
相关题目
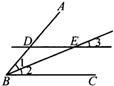16、请把下列证明过程补充完整：
21、请把下列解题过程补充完整并在括号中注明理由：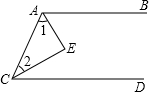
将下列推理过程补充完整，并在括号里填写这一步的根据，如图，AB∥CD，∠BAE=∠DCE=45°，求∠E的大小．
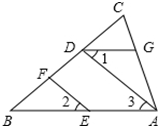把下列推理过程补充完整．