Question

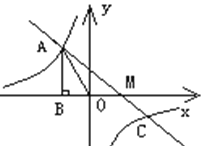
【题目】已知，反比例函数的图象过第二象限内的点，轴于，面积为3，若直线经过点，并且经过反比例函数的图象上另一点.

(1)求反比例函数的解析式；

(2)求直线解析式

(3)求的面积；

(4)直接写出不等式的解集.

Answer 1

【答案】(1)反比例函数为；(2)直线的解析式为:；(3)的面积；(4).

【解析】

（1）根据Rt△AOB面积为得到a＝3，则A点坐标为（2，3），把A点坐标代入可得k＝2×3＝6，确定反比例函数的解析式为；；

（2）把C点坐标代入反比例函数的解析式可确定C点坐标为，然后利用待定系数法确定经过A点和C点的直线解析式；

（3）先求出M点的坐标，然后利用S△AOC＝S△AOM＋S△COM进行计算即可；

（4）由A、C两点的坐标可直接得出不等式的解集．

(1)∵面积为3，，

∴，即，

∴，

∵反比例函数为过点，

∴，即反比例函数为:，

∵反比例函数为，

(2)∵点在反比例函数上，

∴

∴.

∵直线经过点

∴

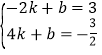
解得：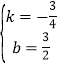

∴直线的解析式为:.

（3）连OC，

对于，令y＝0，则，解得x＝2，

∴M点的坐标为（2，0），

∴S△AOC＝S△AOM＋S△COM＝×2×3＋×2×＝；

（4）∵A（2，3），C（4，），

∴由函数图象可知，不等式的解集是x≤2或0＜x≤4．